Question

Question #f38e0

Answer 1

The weight must be placed at the 32 cm mark.

Explanation:

In order for your stick to be in equilibrium, you need to have a balance between the torque caused by the weight of the stick and the torque caused by the added weight.

Torque is used to express the tendency of a force to produce rotation.

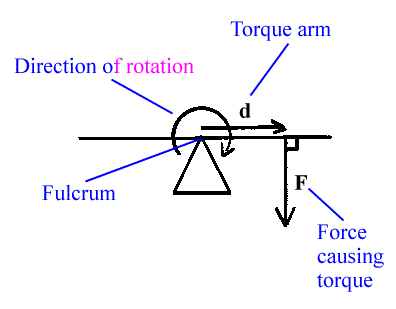
In your case, the clockwise torque caused by the weight of the stick acting on the stick's center of mass will have to be equal to the counterclockwise torque caused by the added weight.

The equation for torque looks like this

`tau = F * d`, where

`F` - the force that's causing the torque;
`d` - the length of the torque arm.

In your case, the fulcrum is placed at the 40 cm mark. Let's say that you place the weight at a distance equal to `x` from where the fulcrum lies - closer to the left side of the stick.

The stick's center of mass is located at the 50 cm mark.The two torques arms will thus be equal to

• `x` cm for the counterclockwise torque;
• `"50-40=10"` cm for the clockwise torque.

This means that torque equilibrium looks like this

`tau_"counterclockwise" = tau_"clockwise"`

`1cancel("N") * x = 0.8cancel("N") * "10 cm"`

`x = 0.8 * 10 = "8 cm"`

Since `x` represents the distance from the fulcrum to the left side of the stick, the weight must be placed at

`x_"weight" = 40-8 = color(green)("32 cm")`