Question #c6d6a
2 Answers
Time of flight
Maximum vertical height
Horizontal range
Explanation:
Your projectile is fired with an initial velocity of 22 m/s and at an angle of
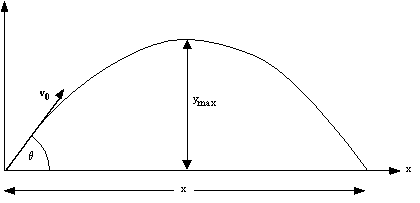
This means that the motion of the projectile has a vertical component and a horizontal component.
Vertically, the projectile will be acted upon by the gravitational acceleration,
In your case
The equation becomes
The only acceptable solution is
At the maximum vertical height, the vertical component of the velocity is zero. This means that you can write
Solving this equation for
Horizontally, the projectile is not acted upon by any forces. This means that you can write
Use the values you have to solve for
1) time of flight =2.44sec 2) maximum vertical height= 7.30 metre
3)horizontal range= 82.6
Explanation:
it is defined as the time taken by any object to travel in any medium it is calculated by
t=2vsintheta/a
maximum vertical height is the peak of that projectile motion the object is travelling
horizontal range it is the range of horizontal motion which is done by object

