(I moved this into Energy Change in Reactions since the varying #K# or #k# value is coupled with varying temperatures, and molecules move at different speeds at different temperatures, and so are differently energetic. Thus, #DeltaT# is proportional to #DeltaE#.)
There's a useful equation we can use.
#ln((K_(p2))/(K_(p1))) = -(DeltaH_R)/R[1/(T_2) - 1/(T_1)]#
and its variation:
#ln((K_(c1))/(K_(c2))) = -(DeltaH_R)/R[1/(T_2) - 1/(T_1)]#
where #R = 8.314472*10^(-3) (kJ)/(mol*K)# and #DeltaH_R# is the enthalpy of reaction.
You may also have seen another variation with kinetics:
#ln((k_2)/(k_1)) = -(E_a)/R[1/(T_2) - 1/(T_1)]#
which is very similar, and just contains the rate constants #k_i# and the activation energy #E_a#, and everything else is the same. Anyways:
You can use both values of #K# (or #k#), both values of #T#, and #R# to solve for #DeltaH_R#. If the result is negative, the reaction is exothermic, and vice versa.
You should have seen something like this plot before, which is represented by the above first or second equation (#lnK# vs. #1/T#):
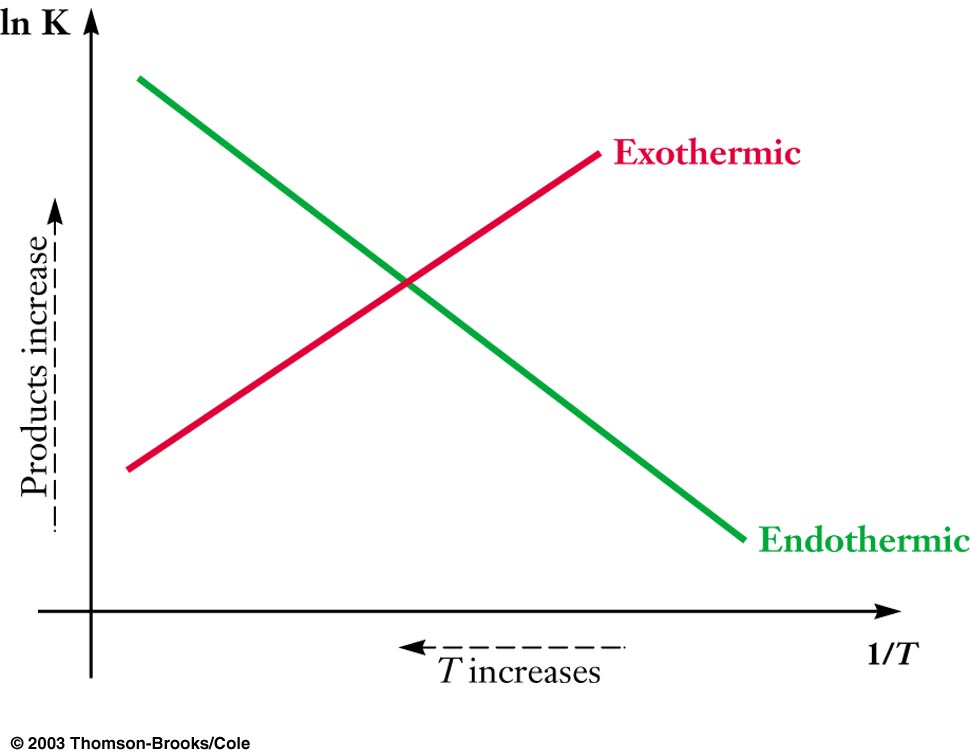
This is derived from the Van't Hoff Equation, #(dlnK)/(dT) = (DeltaH)/(RT^2)#, if you were curious. Just multiply over #dT# and integrate the function from #T_1# to #T_2#. This works well as long as the temperature range is small enough such that #DeltaH# varies linearly with temperature in that range.


