If one bullet is fired at #30^@# and another at #60^@# with respect to the horizontal, given the appropriate amount of time for them both to travel as far as they can and hit the ground, what are their respective ranges?
3 Answers
I tried using "real" values:
Explanation:
Have a look:
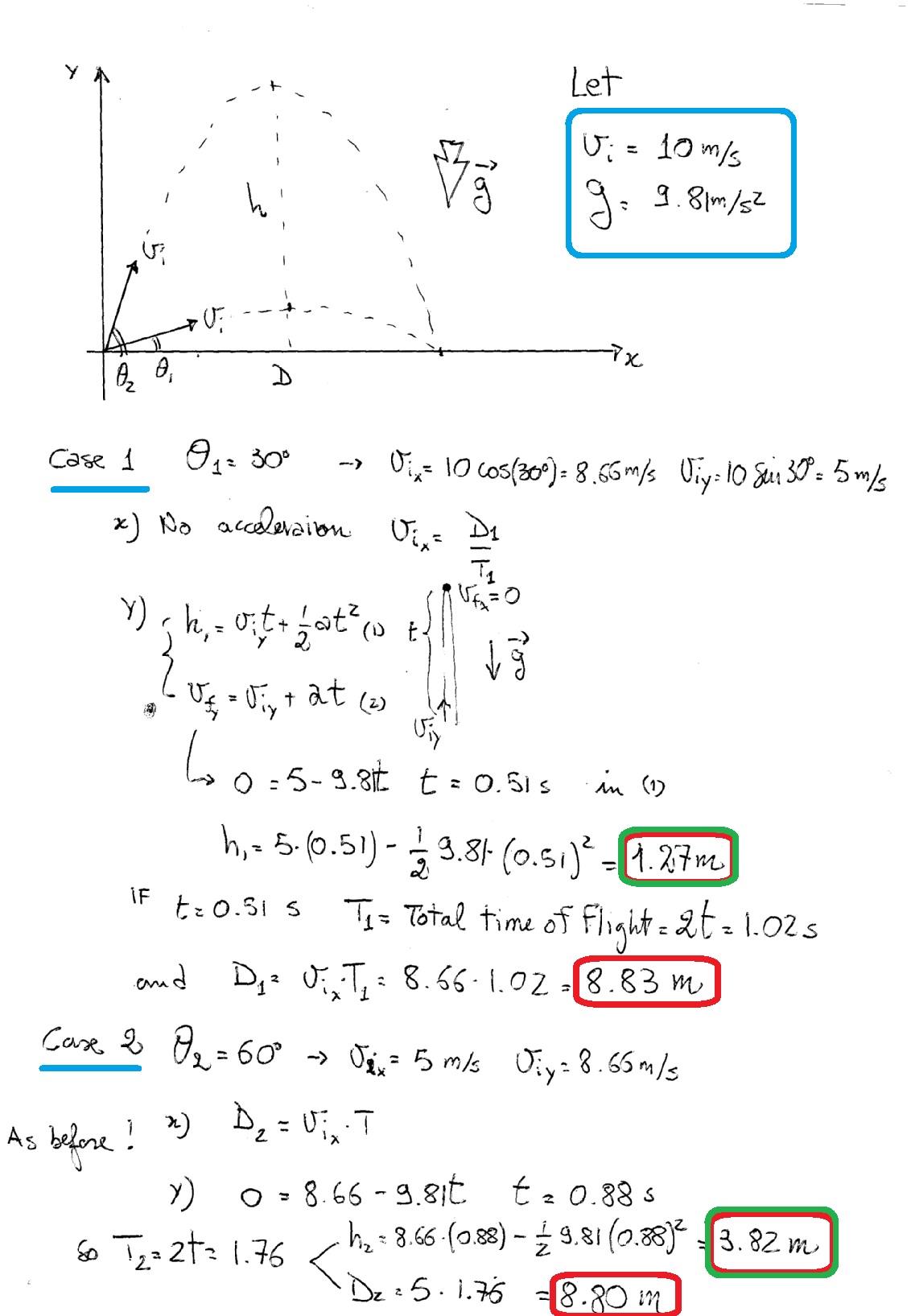
So
These are parabolic motions, and we want
#y_(f1) = -1/2g t_1^2 + v_(y1)t_1 = -1/2g t_1^2 + vsin(30^o)t_1#
#y_(f2) = -1/2g t_2^2 + v_(y2)t_2 = -1/2g t_2^2 + vsin(60^o)t_2#
When the final height is
#0 = -1/2g t_1^2 + vsin(30^o)t_1#
#0 = -1/2g t_2^2 + vsin(60^o)t_2#
With generic, positive
#t_1 = (-v pm sqrt(v^2 - 4(-0.5)(0)))/(2(-0.5))#
#= (-v pm v)/(2(-0.5))#
#= (-v - v)/(-1)#
#= color(green)(v " s") => color(darkgreen)(t_"1/2" = v/2 "s")# .
At this time,
#color(darkred)(y_(f1)) = -g/2(v/2)^2 + (v/2)(v/2) color(darkred)(= (-g/2 + 1) (v/2)^2)#
Compare to
#t_2 = (-(vsqrt3)/2 pm sqrt((vsqrt3/2)^2 - 4(-0.5)(0)))/(2(-0.5))#
#= (-vsqrt3/2 pm vsqrt3/2)/(2(-0.5))#
#= (-(vsqrt3)/2 - (vsqrt3)/2)/(-1)#
#= color(green)(vsqrt3 "s") => color(darkgreen)(t_"1/2" = vsqrt3/2 "s")# .
At this time,
#color(darkred)(y_(f2)) = -g/2 (vsqrt3/2)^2 + (vsqrt3/2)(vsqrt3/2) color(darkred)(= (-g/2 + 1) (vsqrt3/2)^2)#
#color(darkred)(overbrace((cancel(v)sqrt3/cancel(2))^2)^(y_("max",2)) / underbrace((cancel(v/2))^2)_(y_("max",1)) = 3)#
Thus,
For the horizontal distance, let
#x_f = cancel(-1/2 a_x t^2)^(0) + v_xt#
(there is no acceleration due to the gun after the bullet leaves the gun)
#x_(f1) = v_(x1)t_1 = vcos(30^o)t_1#
#x_(f2) = v_(x2)t_2 = vcos(60^o)t_2#
Using the results from earlier (the full time):
#x_(f1) = (v)(sqrt3/2)(v) = sqrt3/2 v^2 "m"#
#x_(f2) = (v)(1/2)(vsqrt3) = sqrt3/2 v^2 "m"#
Thus,

I'll use this equation of motion:
At the zenith
For the projectile launched at
For the projectile launched at
Divide
To get the range we can use:
The times of flight are different but we can get their relationship:
Divide
So
Now substitute this into
If you check the graphic you will see you get the same range whenever you use a complementary pair of launch angles eg 70/20 etc.



