Question #9a3da
2 Answers
Explanation:
As you can see this describes a circle:
graph{x^2+y^2-y-3=0 [-10, 10, -5, 5]}
The 2 tangents where the line
We can find
To get the gradients, we can differentiate both sides implicitly since both
If
Factorising:
If
If
So these are the 2 values of
Now to get the equation of the 1st tangent where
To get
The equation for the tangent
Now to get the 2nd tangent:
To get
The equation becomes:
At the intersection of the 2 tangents we can put
Now to get the
So the (x,y) co-ordinates of the intersection are
To get the angle of intersection between the 2 tangents there is an expression you can use but I think its best to look at the geometry to see what's going on:
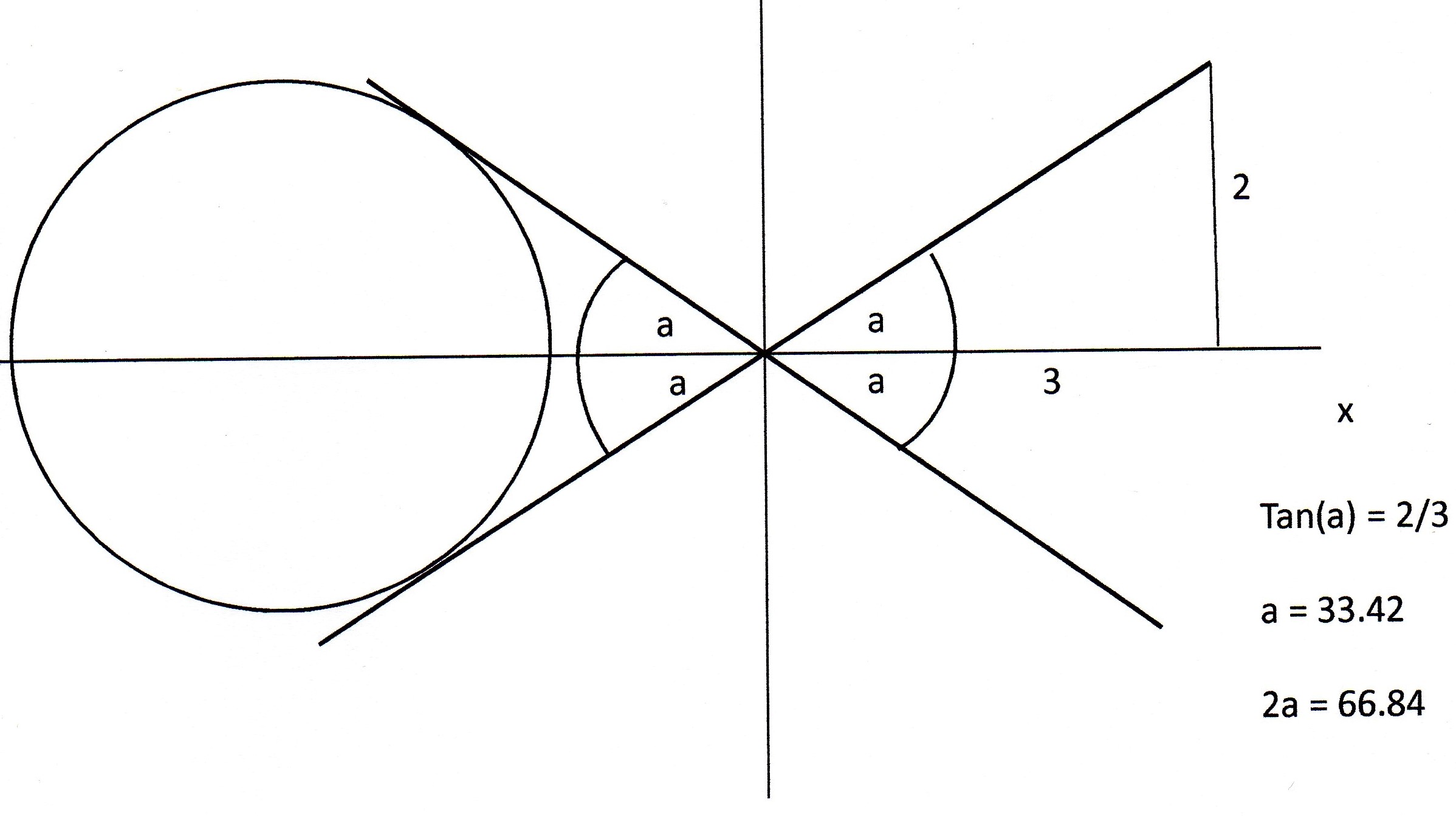
Here you can see that the angle of intersection is
Michael has given a fine answer using a bit of calculus. Here is a partial answer without calculus.
Explanation:
The circle
The center of the circle is
The points on the circle with
To find the slopes of the tangent lines at these points, use the fact that a tangent to a circle at a point is perpendicular to the radius at that point.
At
So the slope of the tangent at
See Michael's answer to get the equation of the tangent line at
At
So the slope of the tangent at
See Michael's answer to get the equation of the tangent line at
For the remainder of the solution, see Michael's answer.


