Definition of the Tangent Line
Key Questions
-
Given two points:
#A(x_A,y_A)# and#B(x_B,y_B)# the line that passes through them is:#(y-y_A)/(y_B-y_A)=(x-x_A)/(x_B-x_A)# . -
A tangent line can be defined as the equation which gives a linear relationship between two variables in such a way that the slope of this equation is equal to the instantaneous slope at some (x,y) coordinate on some function whose change in slope is being examined.
In essence, when you zoom into a graph a lot, it will look more and more linear as you keep zooming in. Then, if you draw a straight line that traces what appears to be a linear function at that zoom, that is the tangent line. That is another way of saying:
#lim_(h->0) (f(x+h) - f(x))/h#
where#h# is essentially a small#Deltax# .The following example uses an early Calculus concept but is fairly easy to figure out:
Let
#f(x) = x^2# . The derivative of#x^2# (the slope of the tangent line), according to the Power Rule, is#(2)*x^((2)-1) = 2x# . Let's say we looked at#f(x) = x^2# at an x value of#7# . There is something called the Newton Approximation Method which gives a straightforward expression for the tangent line.Let
#f_T (x)# be the function of the tangent line, and let#a# be some arbitrary x value. Here, we are assuming it is#7# .#f_T(a) = f'(a)(x-a) + f(a)# As stated earlier, the derivative of
#x^2# is#2x# . That is,#2x# evaluated at each value of#x# is the slope evaluated at each value of#x# for#x^2# . You can see that#x^2# is curved, not linear, and that indicates a changing slope. If#x^2# was a straight line,#2x# would be perfectly horizontal.Plugging in the relevant stuff:
#f_T(7) = f'(7)(x-7) + f(7) = (2*7)(x-7) + (7^2) = 14(x-7) + 49 = 14x-98+49 = 14x-49# If you graph
#f_T(x)# and#f(x)# ,#f_T(x)# will touch the point#(7,49)# on#f(x)# . -
Answer:
A secant line is a straight line joining two points on a function. (See below.)
Explanation:
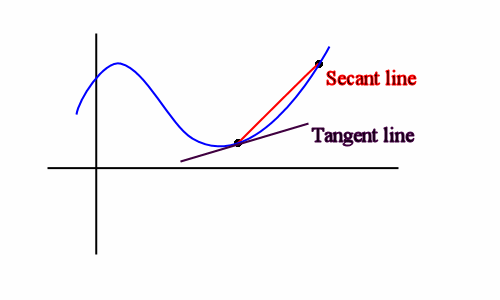
Hope that helped
Source: http://clas.sa.ucsb.edu/staff/lee/secant,%20tangent,%20and%20derivatives.htm
-
You find the tangent line of a function by finding the derivative, the slope, of that function at a specific point.
That point is called the point of tangency.
Substitute that point and the derivative into the slope intercept formula,
#y=mx+b# , to find the#y# -intercept.Lastly, the equation of the tangent line is found by substituting in the derivative and
#y# -intercept into the slope intercept formula,#y=mx+b# .