Question

Question #31f40

Answer 1

`P_"sol" = "310 mmHg"`

Explanation:

In order to be able to solve this problem, you need to know what the vapor pressure of pure ethanol is at `45^@"C"`.

The curve that depicts methanol's vapor prssure versus temperature looks like this

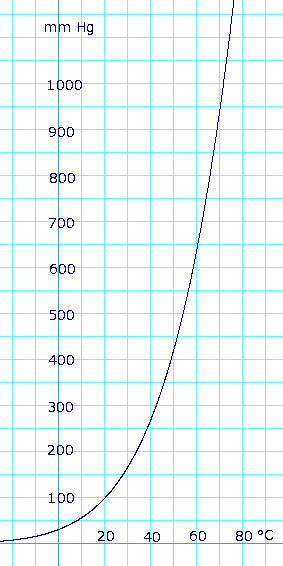
Accoding to this curve, methanol has a vapor pressure of about `"333 mmHg"` at `45^@"C"`. If you want a more accurate value, use this calculator based on the Antoine equation (I won't go into that here)

http://ddbonline.ddbst.de/AntoineCalculation/AntoineCalculationCGI.exe

So, you know that you solution contains `"4.50 moles"` of methanol and `"0.35 moles"` of glycerol.

According to Raoult's Law, you can estimate the vapor pressure of a solution by using the mole fraction of the solvent in said solution, and the vapor pressure of the pure solvent at the same temperature.

In other words, the vapor pressure of your solution can be calculated by using the mole fraction of methanol and its vapor pressur at `45^@"C"`.

`P_"sol" = chi_"methanol" * P_"methanol"^0`

The mole fraction of a component in a mixture or solution is defined as the number of moles of that respective substance divided by the total number of moles in the solution.

The total number of moles in the solution will be

`n_"total" = n_"methanol" + n_"glycerol"`

`n_"total" = "4.50 moles" + "0.35 moles" = "4.85 moles"`

The mole fraction of methanol will thus be

`chi_"methanol" = (4.50color(red)(cancel(color(black)("moles"))))/(4.85color(red)(cancel(color(black)("moles")))) = 0.9278`

This means that the vapor pressure of the solution will be

`P_"sol" = 0.9278 * "333 mmHg" = "308.96 mmHg"`

Rounded to two sig figs, the answer will be

`P_"sol" = color(green)("310 mmHg")`