Question

Explain what quantum tunnelling is?

Answer 1

Ok, this is steep but I'll try...

Explanation:

If you run against a wall you can predict with `100%` accuracy that you'll end up with a headache; the probability you can pass through the wall is quite low...but what if you are an electron?
This is a bit more complicated because it is difficult to say WHERE you are in the first place!
The only thing you can say is that there is a certain probability, say `60%`, that you are at a certain position. This is because you, as an electron, are now a wave-particle entity that Quantum Physics describes only from the point of view of probabilities.

Now, you are an electron running against a barrier (a potential barrier, such as a wall charged negatively that for the electron is the same as a brick wall for a person) and you do not pass (you are reflected back) because again the probability to find you beyond the barrier is very small (say `0.0000000000000000001%`)...but now you can call in other billions of billions of electrons and all run against the wall....Quantum Physics then evaluates the probability of finding one electron beyond the barrier...and finds one of them!!!!!

Basically, Quantum Mechanical entities are dominated by probability and, being very small, can operate in huge numbers so that even filmsy probabilities in our big world become quite acceptable microscopically!

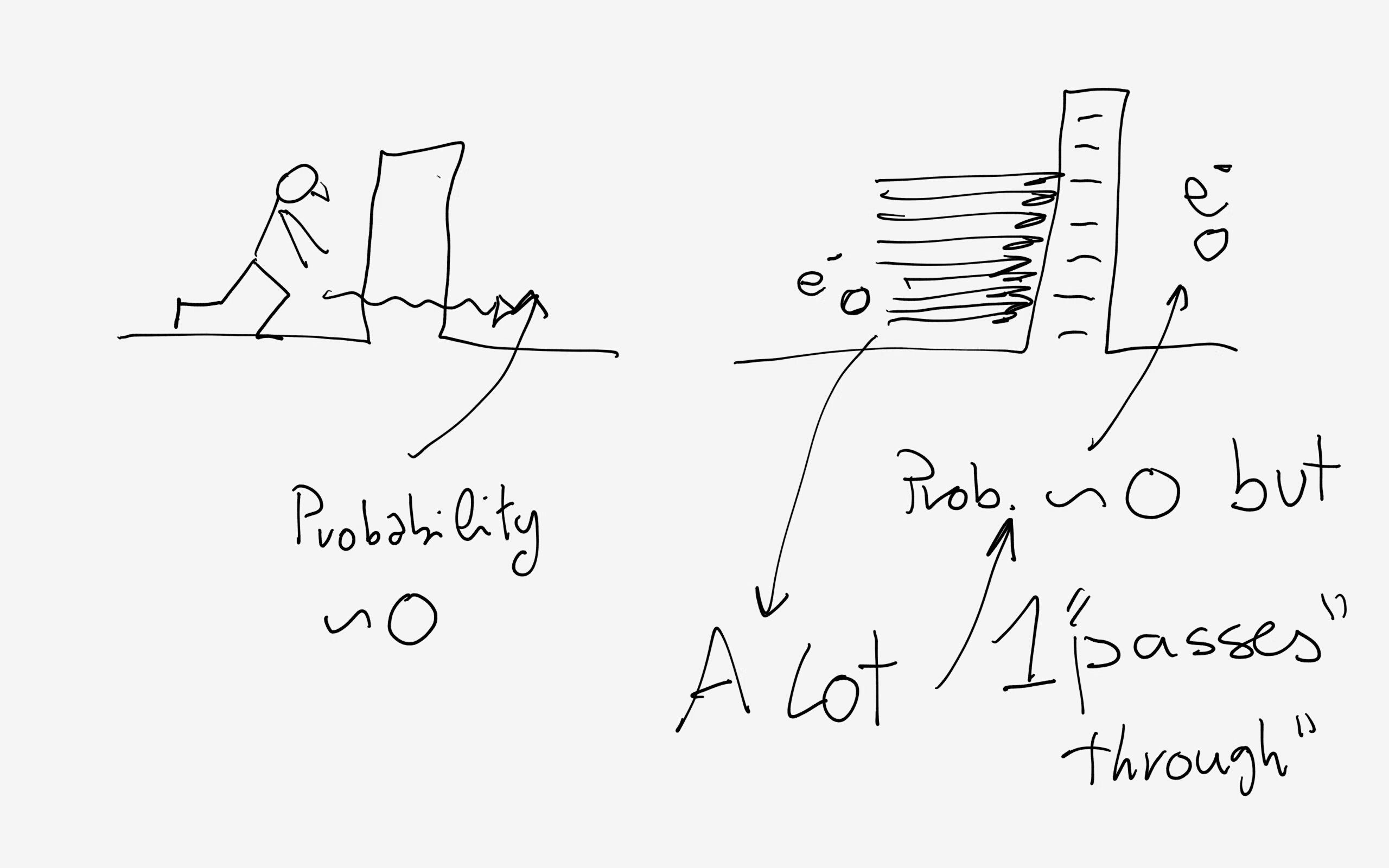
Hope it is not too confusing!

Answer 2

QUICK INTRO INTO QUANTUM TUNNELING: WHAT DOES IT ACCOUNT FOR?

Some more common events where quantum tunneling is an underlying factor (Physical Chemistry: A Molecular Approach, McQuarrie, pg. 144):

• `alpha`-decay of nuclei
• electron-transfer reactions
• hydrogen bonding

THE PREDICTIONS OF CLASSICAL VS QUANTUM MECHANICS

Let's say we had a high probability that some electrons are right in front of a potential energy barrier (with `V_0` for potential energy). In order for one of them to make it over the barrier, classical mechanics states that it should have kinetic energy `\mathbf(K > V_0)`.

However, quantum mechanics states that it's fine if `\mathbf(K < V_0)` for particles like the electron. Why is that? Well, mainly because the electron has both wave and particle properties.

SETTING UP THE SCENARIO

For simplicity, consider the `x` direction, and let the electrons be in a space with `Deltay -> oo`. That is, let the electrons be confined into a two-dimensional plane of infinite physical height but finite physical width.

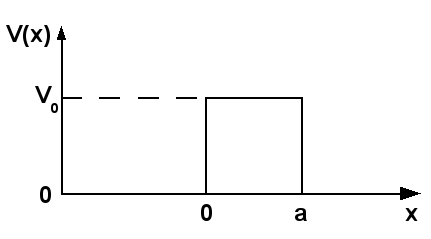
(This is also called the Particle in a Box, or Square Well scenario.)

This is perplexing, because normally we humans wouldn't be able to get out unless we had enough energy (that is, if `K > V_0`). We can't just climb out because we already supposed that `Deltay -> oo`.

HOW MIGHT THE ELECTRON "TUNNEL" OUT?

Since this potential energy barrier is infinitely high and the only way to get past it is to go through it, the electrons have to either break the barrier somehow, or transmit themselves through the barrier and into a new space.

This barrier is massless (because energy is massless), so the electrons can't simply break the barrier (only tangible things can be broken).

Interestingly enough, since an electron can act as a wave, it can be either transmitted through the barrier or reflected back by the barrier. There's a probability for each to happen.

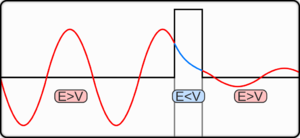
Therefore, to make it through, they have to "magically" tunnel through the barrier. (Afterwards, other nearby electrons would move a bit faster to account for conservation of energy.)

THE TRANSMISSION PROBABILITY OF THE ELECTRON

We call the probability of this quantum tunneling event the Transmission Probability, since particles as small as an electron have to be described via probabilities (note the Heisenberg Uncertainty Principle).

Based on the derivation from this answer, the transmission coefficient (or probability) can be graphed as a function of the relative electron energy `E` compared to the height of the potential energy barrier `V_0`.

In the graph I chose `v_0 = (2ma^2V_0)/ℏ^2 = 10` for `epsilon = (2ma^2E)/ℏ^2`, with `epsilon//v_0 = E//V_0`:

With `V_0` being the potential energy, the x-axis (`E"/"V_0`) is in units of `V_0`, so:

• If we are at `1` on the x-axis, `K = V_0`. At that point, the probability of the electron tunneling through the barrier is small but nonzero. It's actually about `\mathbf(20%)` (Physical Chemistry: A Molecular Approach, McQuarrie, pg. 144).
• If we are at `2.5` on the x-axis, `K = 2.5V_0`. At that point, the probability of the electron tunneling through the barrier is about `\mathbf(90%)` or so.

This indicates that some electrons can pass through this infinitely high potential energy barrier at `~\mathbf(20%)` probability if they have nearly enough energy, or even `~\mathbf(100%)` of the time at `\mathbf(~2)` times the necessary energy.

(A big basketball wouldn't be able to do this, because it would behave according to classical mechanics. Quantum mechanics applies best for very, very small particles like the electron.)

Answer 3

In words, no equations

Explanation:

In classical physics, if you're behind a wall, you stay behind a wall. It doesn't matter that the wall has finite height, if it is higher than you, you stay put. It is not impossible to be on the other side, in principle, but it won't happen. In quantum physics if it is not impossible it is happening.

Remember there are no shortest path in quantum physics. The particle goes through all paths at the same time. Since it behaves like a wave, it will interfere with itself and the result will look like a classical shortest path, but it's not. And if a path is not impossible, it will be taken, that is, it has been taken. The wall is not infinite, part of you is on the other side, but not much. Inside the wall your amplitude has decreased exponentially.

This is due to the fact that your energy being negative inside the wall, the wave function that describes you is the solution of the Schrodinger's Equation with negative energy is that of a diffusion equation (the heat equation) and is no longer a wave.