Question

Question #6b9d0

Answer 1

In fact the ratio is `7/19`

Explanation:

Refer to the figure below

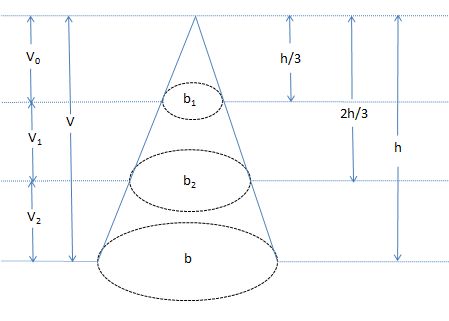
Since the 2 planes divide the cone in 3 parts we can obtain 3 ratios. But I presume that `V_1/V_2` is what is intended.

Just not to create confusion, be noticed that `b, b_1 and b_2` are the areas (in square units) of the bases of their respective cones.

The volume of a cone is given as
`V=(S_(base)*height)/3`

Finding `V_2`

`V_2=V-(V_0+V_1)=(bh)/3-(b_2*(2h)/3)/3=(bh)/3-2/9*(b_2*h)`
Notice that
`->(b_2)/b=(pi*r_2^2)/(pi*r^2)=(r_2/r)^2` and since `r_2/r=((2cancel(h))/3)/cancel(h)=2/3`
`=>(b_2)/b=(2/3)^2` => `b_2=4/9*b`
So
`V_2=(bh)/3-2/9*(b_2*4/9b)=(27bh-8bh)/81` => `V_2=(19*bh)/81`

Finding `V_1`

`V_1=V-V_0-V_2=(bh)/3-(b_1*h/3)/3-(19*bh)/81`
But as we saw above
`b_1/b=((cancel(h)/3)/cancel(h))^2=(1/3)^2` => `b_1=b/9`
So
`V_1=(bh)/3-b/9*h/9-(19*bh)/81=(27*bh-bh-19*bh)/81` => `V_1=(7*bh)/81`

So the asked ratio is

`V_1/V_2=((7*cancel(bh))/cancel(81))/((19*cancel(bh))/cancel(81))=7/19`