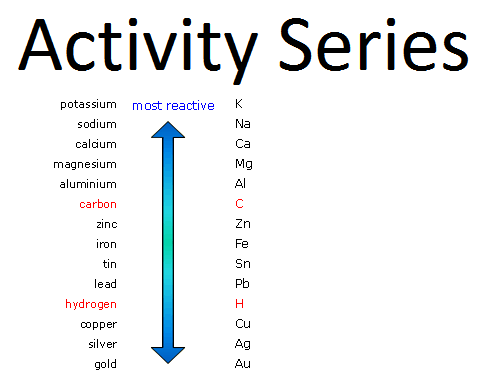First you need to tally all the atoms involved in the reaction.
#Na# + #Ca_3(PO_4)_2# #rarr# #Na_3PO_4# + #Ca# (unbalanced)
left side:
#Na# = 1
#Ca# = 3
#(PO_4)# = 2
right side:
#Na# = 3
#Ca# = 1
#(PO_4)# = 1
Notice that I enclosed the #PO_4^"3-"# ion in parentheses to denote the covalent bonding between them.
Start balancing the equation from easiest to hardest. In this case, the #PO_4^"3-"# ion.
#Na# + #Ca_3(PO_4)_2# #rarr# #color (red) 2Na_3PO_4# + #Ca#
left side:
#Na# = 1 x
#Ca# = 3
#(PO_4)# = 2
right side:
#Na# = 3 x #color (red) 2# = 6
#Ca# = 1
#(PO_4)# = 1 x #color (red) 2# = 2
Notice that since #Na_3PO_4# is a substance, you need to apply the coefficient, not only with the phosphate ion, but also to #Na#.
#color (blue) 6Na# + #Ca_3(PO_4)_2# #rarr# #color (red) 2Na_3PO_4# + #Ca#
left side:
#Na# = 1 x #color (blue) 6# = 6
#Ca# = 3
#(PO_4)# = 2
right side:
#Na# = 3 x #color (red) 2# = 6
#Ca# = 1
#(PO_4)# = 1 x #color (red) 2# = 2
Now the only element left to balance is the #Ca#.
#color (blue) 6Na# + #Ca_3(PO_4)_2# #rarr# #color (red) 2Na_3PO_4# + #color (green) 3Ca#
left side:
#Na# = 1 x #color (blue) 6# = 6
#Ca# = 3
#(PO_4)# = 2
right side:
#Na# = 3 x #color (red) 2# = 6
#Ca# = 1 x #color (green) 3# = 3
#(PO_4)# = 1 x #color (red) 2# = 2
The equation is now balanced.
Note:
This reaction is called a single displacement reaction wherein the more reactive element "displaces" the less reactive one in the chemical equation.
In order to know which element is more reactive, you would need to familiarize yourself with the activity series of metals.
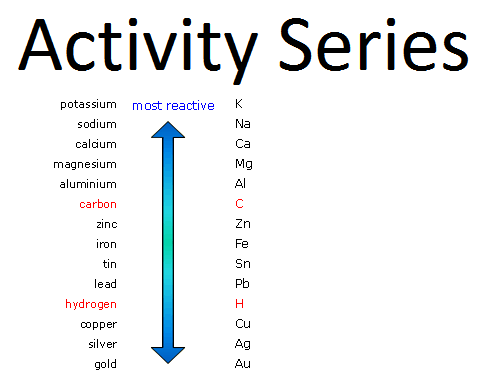
I'm including this little fact since not all displacement reactions proceed as predicted. For example, if the equation is #Ca# + #Na_3PO_4# #rarr# ?
it would yield no reaction.
#Ca# + #Na_3PO_4# #rarr# no reaction