Basically yes. The angular momentum quantum number l corresponds to the shape of the orbital sublevel, and the magnetic quantum number m_l basically "builds" the shape when the p electron is subjected to a magnetic field.
But for the most part you can say that l indicates the shape because different values of l correspond to different orbital shapes.
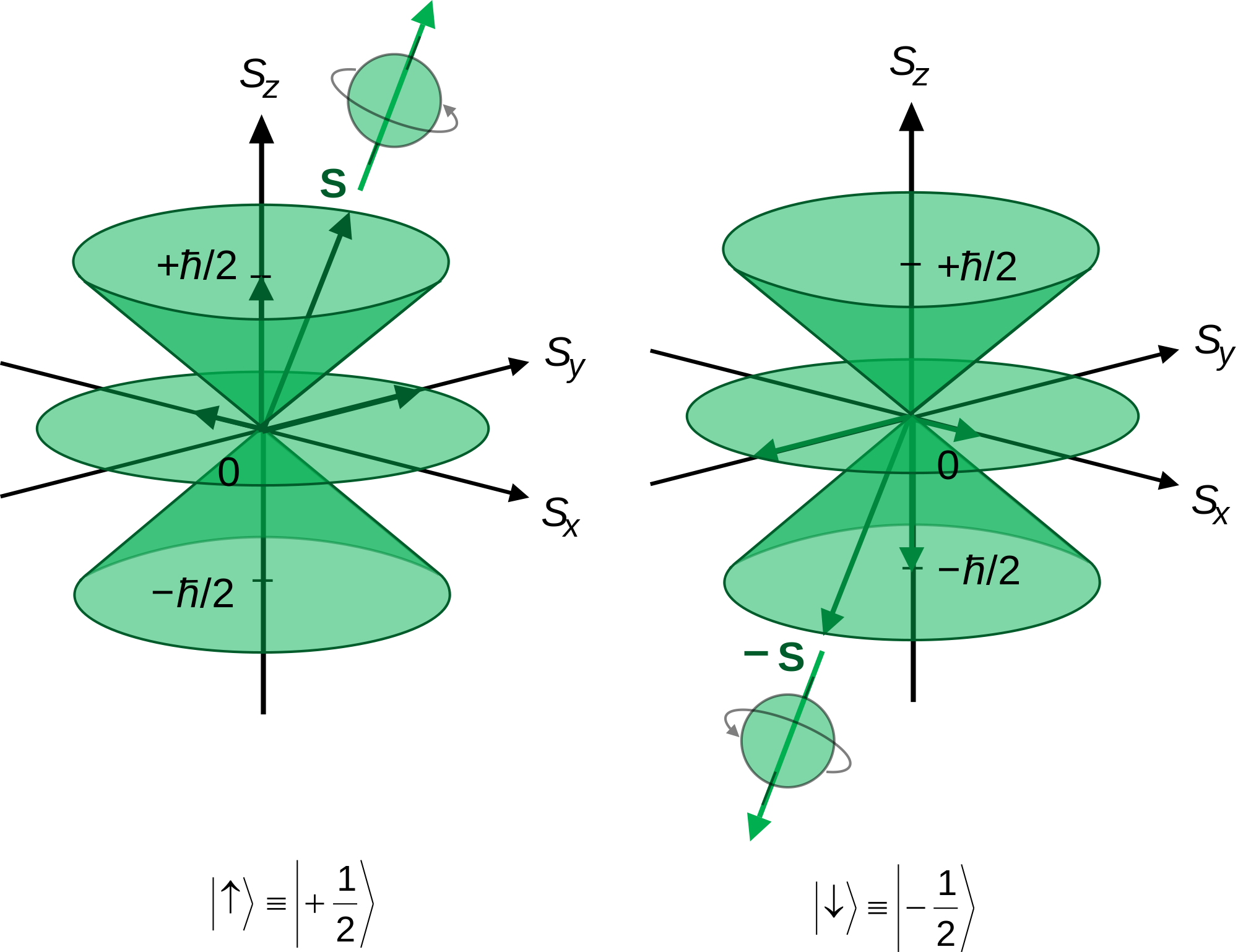
If we take the 2p_z orbital as an example and subject it to a magnetic field oriented in the z direction, the orbital angular momentum in the z direction sweeps out cones like this:
 )
)
(Ignore the "|uarr>>" and "|darr>>"; it is not relevant, though it is called bra-ket notation if you look it up and bother to read more on it! Also, you would not have to explain this diagram on a General Chemistry test. In case you were curious though, the diagram shows ℏ"/"2, which is the height of the cones in units of ℏ. Anyways...)
Looks like a 2p_z orbital, right? It should.
The orbital angular momentum in the z direction is L_z. In the following equation (which you don't need to use on a General Chemistry test):
color(blue)(hatL_z)Y_l^(m_l)(theta,phi) = color(blue)(m_lℏ)Y_l^m(theta,phi)
What you should notice here is that hatL_z, the orbital angular momentum operator for the z-direction, corresponds to m_lℏ.
If n = 2, l = 1 corresponds to a 2p atomic orbital, so m_l = 0, pm1.
- The -1 refers to the lower cone on the above image.
- The 0 refers to a dot at the origin in the above image. It is also where the node is.
- The +1 refers to the upper cone in the above image.
This tells us that m_l is also known as the vector projection of l.
Therefore, what you should notice is that m_l "builds" the shape of the orbital, while the number of m_l values corresponds to how many unique, orthogonal (perpendicular) orientations there are for any orbital in that sublevel.
(The orthogonality is not crucial knowledge for General Chemistry, but it matters because a quantum mechanics postulate states that any orbital must be orthogonal to every other orbital in its sublevel.)
Ultimately, since there are three values for m_l, there are three 2p orbitals: 2p_x, 2p_y, and 2p_z.
 )
) 
