Question

How many electrons have `n = 3`, `l = 2`?

Answer 1

`"10 e"^(-)`

Explanation:

As you know, quantum numbers are used to describe the location and spin of an electron in an atom.

A total of four quantum numbers are used for this purpose, three describing the location of the electron and one describing its spin.

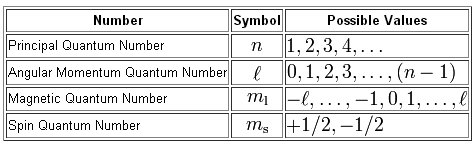
Now, you are given the values of two quantum numbers, the principal quantum number, `n`, and the angular momentum quantum number, `l`.

The principal quantum number tells you the energy level on which the electrons reside. In your case, `n=3` tells you that you can find these electrons on the third energy level.

The angular momentum quantum number tells you the subshell in which you can find these electrons. The possible values of `l` for the third energy level are

• `l=0 ->` the s-subshell
• `l=1 ->` the p-subshell
• `l=2 ->` the d-subshell

This means that your electrons are located in the d-subshell, more specifically, in the 3d-subshell.

Now, to determine how many electrons can share these two quantum numbers, identify how many orbitals you have in the d-subshell.

This value is given by the magnetic quantum number, `m_l`. For `l=2`, `m_l` can be

`m_l = { -2; -1; color(white)(-)0; color(white)(-)1; color(white)(-)2}`

So, if the d-subshell can hold a maximum of five orbitals, and you know that each orbital can hold a maximum of two electrons, it follows that a total of

`"no. of electrons" = 2 xx 5 = "10 e"^(-)`

can share the two quantum numbers `n=3` and `l=2`.