If #h# is the height the object moves up the plane and #l# is the slant distance moved along the plane and #d# is the run.
#h/l=sintheta#
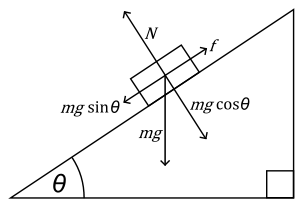
Force of friction #F_f=muN=mumg cos theta#
Where #mu# is the coefficient of dynamic friction
#m# is the mass
#g# is gravity
#theta# is the angle above horizontal
Work done against friction:
#"work done" = "force due to friction" xx "distance moved "l#
#= (muxxmgcostheta) xx l#
When the object comes to stop, part of its Kinetic energy #E# got converted into its potential energy and rest of it has been used to overcome kinetic friction.
#mgh=E- mumgcos thetaxxl#
#mglsintheta=E- mumgcos thetaxxl#, solving for #l#
#=>l =E/(mgsintheta+mumgcostheta)#
Again
#"work done" = "force due to friction" xx "distance moved "l#
#= (muxxmgcostheta) xx l#
#=(muEmgcostheta)/(mgsintheta+mumgcostheta)=
(muEcostheta)/(sintheta+mucostheta)#

