Question #dcf44
1 Answer
Here's what I got.
Explanation:
Your strategy here will be to determine the volume of the unit cell by using the given edge length, use gold's density to determine the mass of the unit cell, then use the mass of a single gold atom to determine how many atoms you get per unit cell.
So, the first important thing to notice here is that the density of gold is given in grams per cubic centimeters, but that the length of the unit cell is given in picometers.
This means that you're going to have to convert the length of the cell to match that used for density. Use the fact that
#"1 pm" = 10^(-12)"m" = 10^(-10)"cm"#
to get
#407.9color(red)(cancel(color(black)("pm"))) * (10^(-10)"cm")/(1color(red)(cancel(color(black)("pm")))) = 4.079 * 10^(-8)"cm"#
As you know, the volume of a cube is given by the formula
#color(blue)(V = l xx l xx l = l^3)" "# , where
Plug in the value you have for the length of the cubic unit cell to get
#V = (4.079 * 10^(-8))^3 "cm"^3 = 6.787 * 10^(-23)"cm"^3#
Use the density of gold to determine the mass of a cubic unit cell
#6.787 * 10^(-23)color(red)(cancel(color(black)("cm"^3))) * "19.3 g"/(1color(red)(cancel(color(black)("cm"^3)))) = 1.31 * 10^(-21)"g"#
Now all you have to do is determine how many atoms of gold you could fit in the unit cell. To do that, use gold's molar mass, which tells you what the mass of one mole of gold atoms is.
Since you're interested in finding the mass of a single gold atom, divide the molar mass by Avogadro's number, which tells you the number of atoms you get per mole of an element.
#196.97"g"/color(red)(cancel(color(black)("mole of Au"))) * overbrace((1color(red)(cancel(color(black)("mole Au"))))/(6.022 * 10^(23)"atoms"))^(color(green)("Avogadro's number")) = 3.271 * 10^(-22)"g/atom"#
Now, if your unit cell has a mass of
#1.31 * 10^(-21)color(red)(cancel(color(black)("g"))) * "1 atom of Au"/(3.271 * 10^(-22)color(red)(cancel(color(black)("g")))) = 4.0049 ~~ color(green)("4 atoms of Au")#
Now, when it comes to cubic lattice structures, you can only deal with three possible sub-types
- a simple cubic structure
- a body-centered cubic structure
- a face-centered cubic structure
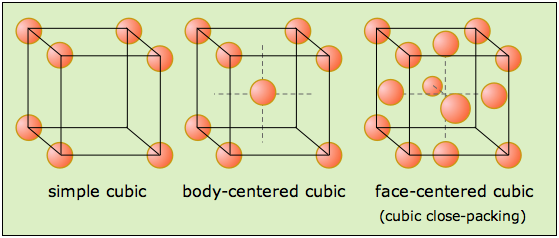
Now, take a look at those three possible unit cells. Notice that they all have lattice points in the corners of the cube.
Each of these lattice points contains
For a face-centered cubic cell, each face contains
#"no. of atoms" = overbrace(1/8 xx 8)^(color(red)("8 corners")) + overbrace(1/2 xx 6)^(color(green)("6 faces")) = "4 atoms"#
And there you have it, gold has a face-centered cubic lattice structure.

