Question #72e37
1 Answer
Here's what I got.
Explanation:
It's worth noting that all of these decay types will result in nuclear transmutation, i.e. the atoms of the elements that are undergoing radioactive decay will be converted to atoms of different elements.
Plutonium-242 will undergo alpha decay, which means that its nucleus will emit an alpha particle.
An alpha particle is essentially the nucleus of a helium-4 atom,
This tells you that the resulting isotope will have an atomic number equal to
Z = 94 - 2 = 92
and a mass number equal to
A = 242 - 4 = 238
A quick look in the periodic table will reveal that the resulting isotope is uranium-238
""_94^242"Pu" -> ""_92^238"U" + ""_2^4alpha
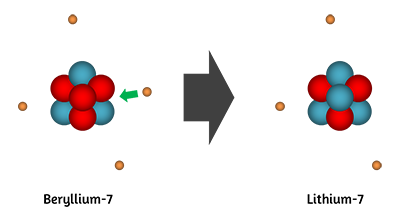
Beryllium-7 will decay via electron capture, during which an inner-orbital electron is being captured by the nucleus.
This process leads to the conversion of a proton to a neutron and the emission of an electron neutrino. As a result, the nucleus' atomic number will decrease by
So, the resulting isotope will have
Z = 4 - 1 =3" " and" "A = 7
A quick look in the periodic table will show that you're dealing with lithium-7
""_3^7"Be" + ""_text(-1)^0"e" -> ""_3^7"Li" + ""_0^0nu_e
 http://evolutiondismantled.com/accelerated-decay
http://evolutiondismantled.com/accelerated-decay
Finally, oxygen-15 decays via positron emission, also known as
The nucleus will emit a positron, the antiparticle of the electron, and an electron neutrino. Positron emission will decrease the atomic number of the nucleus by
The resulting isotope will have
Z = 8 - 1 = 7" " and" "A = 15
Another quick look in the periodic table will reveal that you're dealing with nitrogen-15.
""_8^15"O" -> ""_7^15"N" + ""_text(+1)^0"e" + ""_0^0nu_e

