If a solvent contains a few impurities, how does its boiling point compare to the pure solvent?
2 Answers
The boiling point of the compound will be slightly elevated.
Explanation:
Usually, the boiling point of a liquid has a rising temperature gradient. Impurities elevate the boiling point, and the elevation is proportional to their concentration.
As the distillation proceeds, the concentration of the impurity (left in the still pot) becomes greater and boiling point becomes higher. A second distillation of the first collected fraction is usually performed, and this gives a much more stable distillation profile in that the distillate is more pure, and a much better measurement of the boiling point may be achieved.
In considering boiling point, we are likely talking about a liquid. When dissolving something unlike the liquid in the liquid, you add impurities into the liquid.
Consider the following expression, derived from the Gibbs-Duhem relation (Physical Chemistry: A Molecular Approach, Ch. 24-2, pg. 968):
#\mathbf(mu_j = mu_j^"*" + RTlnchi_j)# where:
#mu_j# is the chemical potential, or the partial molar free energy, of component#j# in solution. It is similar in principle to potential energy in that substances generally want to minimize chemical potential.#R# is the universal gas constant#T# is temperature in#"K"# #chi_j# is the mole fraction of component#j# in solution. It could be written as#(n_j)/(n_i + n_j)# for a solution containing components#i# and#j# , where#n_j# is the number of#"mol"# s of component#j# .#"*"# is the IUPAC notation for a pure substance, i.e. one that is not mixed with anything other than itself.
WHAT IF WE DISSOLVE SOMETHING IN THE SOLUTION?
If we suppose a liquid organic compound
#mu_j = mu_j^"*" + RT ln (chi_j color(blue)( + x))# where
#x# is the fraction of the solution that is no longer made up of#j# , meaning that#chi_j + x = 1# .
Since
When
Now consider the following diagram, which examines the chemical potential vs. the temperature at a constant pressure:
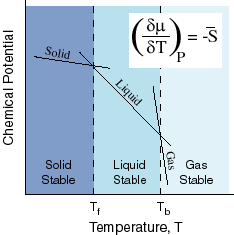
When crossing over to a different phase (e.g. solid
Right now, the graph shows
Since the intersections indicate the boiling and freezing points, the boiling point has shifted to the right, and therefore, the boiling point increases.
This is why there is some boiling point elevation when you dissolve a solute into a solvent.


