Question

Question #c698b

Answer 1

`"0.35 nm"`

Explanation:

Your strategy here will be to use the definition of the unified atomic mass unit, `"u"`, to find the mass of a single nickel atom, then use the characteristics of a face-centered cubic structure to find the total mass of a unit cell.

Once you know the mass of a cell, use nickel's density to determine the cell's volume.

So, the unified atomic mass unit is defined as `1/12"th"` of the mass of a single neutral carbon-12 atom in its ground state and is equal to

`"1 u" = 1.660539 * 10^(-24)"g"`

The mass of a single nickel atom expressed in grams will thus be

`58.7 color(red)(cancel(color(black)("u"))) * (1.660539 * 10^(-24)"g")/(1color(red)(cancel(color(black)("u")))) = 9.747 * 10^(-23)"g"`

Now, a face-centered cubic cell structure is characterized by a total of `14` lattice points distributed as follows

• one lattice point in every corner of the cell `->` a total of eight corner lattice points
• one lattice point in every face of the cell `->` a total of six face lattice points

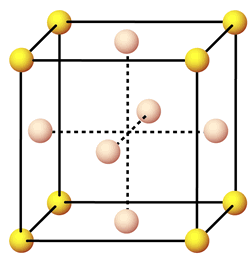
Each corner lattice point will hold `1/8"th"` of an atom and each face lattice point will hold `1/2` of an atom. The total number of atoms of nickel that can be found in a face-centered cubic cell will thus be

`"no. of atoms" = overbrace(1/8 * 8)^(color(blue)("corners")) + overbrace(1/2 * 6)^(color(red)("faces")) = "4 atoms"`

So, if each cell contains a total of `4` nickel atoms ,and each atom has a mass of `9.474 * 10^(-23)"g"`, it follows that the total mass of a cell will be

`4 color(red)(cancel(color(black)("atoms"))) * (9.747 * 10^(-23)"g")/(1color(red)(cancel(color(black)("atom")))) = 3.899 * 10^(-22)"g"`

Use the given density to find the volume of a unit cell

`3.899 * 19^(-22) color(red)(cancel(color(black)("g"))) * "1 cm"^3/(8.9 color(red)(cancel(color(black)("g")))) = 4.381 * 10^(-23)"cm"^3`

As you know, the volume of a cube is given by the formula

`color(blue)(V = l xx l xx l = l^3)" "`, where

`l` - the length of the cube

This means that you have

`l = root(3)(V)`

In your case, this is equivalent to

`l = root(3)(4.381 * 10^(-23)"cm"^3) = 3.525 * 10^(-7)"cm"`

The length of the unit cell is usually given in nanometers, so convert the result to get

`3.525 * 10^(-8) color(red)(cancel(color(black)("cm"))) * (10^7"nm")/(1color(red)(cancel(color(black)("cm")))) = "0.3525 nm"`

Rounded to two sig figs, the number of sig figs you have for nickel's density, the answer will be

`l = color(green)("0.35 nm")`