Question #d4fff
1 Answer
Explanation:
Before doing any calculation, think about what you would expect to see happen to the temperature of the gas sample.
You know that the initial volume of the container is set at
As you know, temperature is a measure of the average kinetic energy of the gas molecules. The higher the temperature, the faster these molecules will move.
Now, the volume of the gas will be proportional to its temperature because the faster the molecules are moving, the more powerful and frequent the collisions between themselves and with the container walls will be.
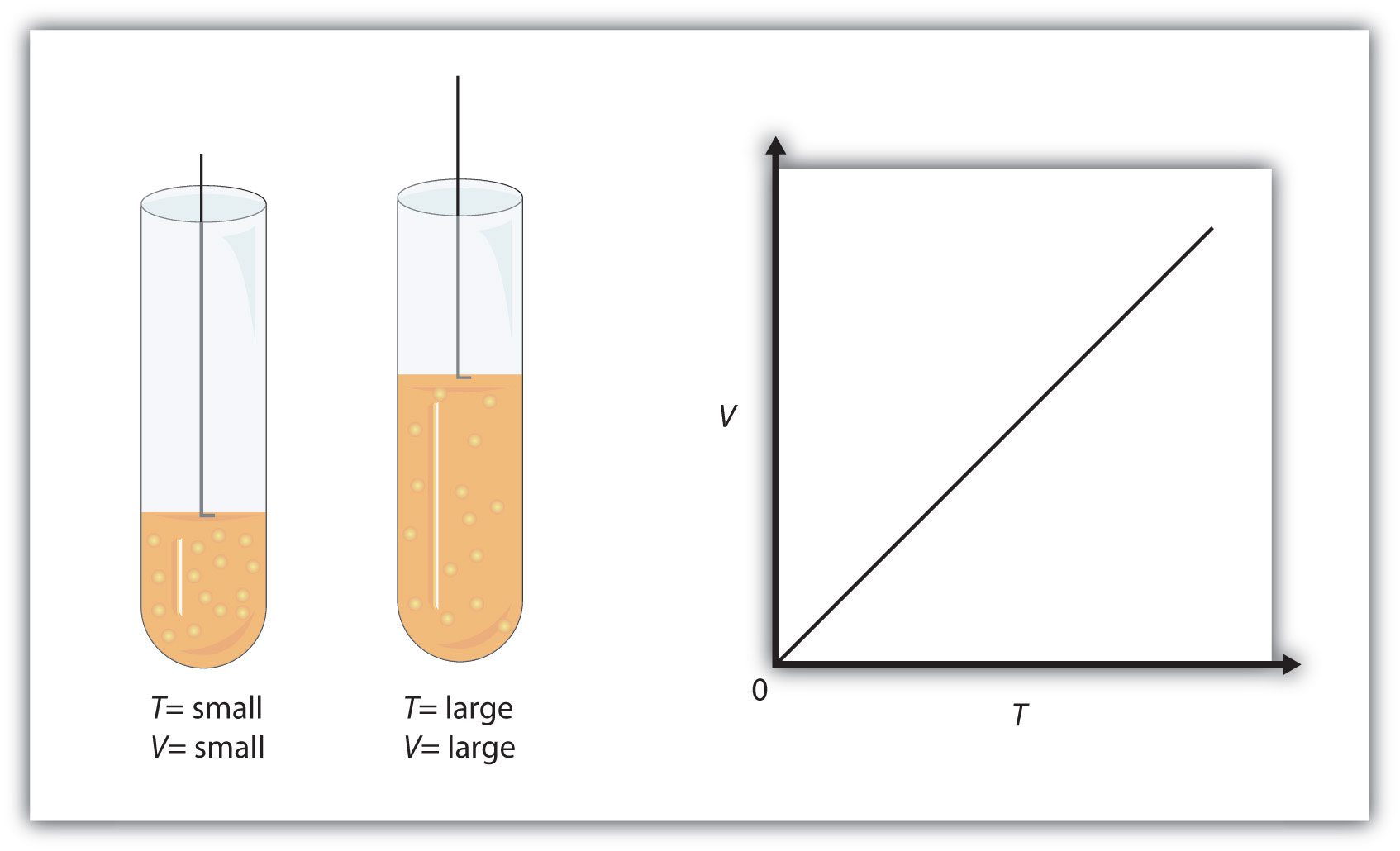
Since pressure is kept constant, the result of increasing the temperature of the gas would be to produce an increase in volume.
This means that decreasing the temperature of the gas will have the opposite effect - gas molecules will now more slower, and their collisions with the walls of the container will not be as frequent and as powerful
Mathematically, this is written as
#color(blue)(V_1/T_1 = V_2/T_2)" "# , where
In your case, the volume decreases, which means that temperature must decrease as well.
#T_2 = V_2/V_1 * T_1#
Do not forget to convert the temperature to Kelvin!
#T_2 = (0.0755 color(red)(cancel(color(black)("L"))))/(1.55 color(red)(cancel(color(black)("L")))) * (273.15 + 32)"K" = "14.864 K"#
You need to round this off to two sig figs, the number of sig figs you have for the initial temperature of the gas.
#T_2 = color(green)("15 K")#

