Question

How do you construct a Born-Haber cycle to calculate the lattice energy of sodium chloride?

Answer 1

By definition, the gaseous cation and anion forming the corresponding ionic compound release energy termed the lattice energy, the energy contained within the lattice structure.

For an alternative explanation, see here.

The Born-Haber cycle takes advantage of the state function property of the change in enthalpy to indirectly determine the lattice energy of ionic compounds through processes that utilize known thermodynamic quantities like ionization energy and electron affinity.

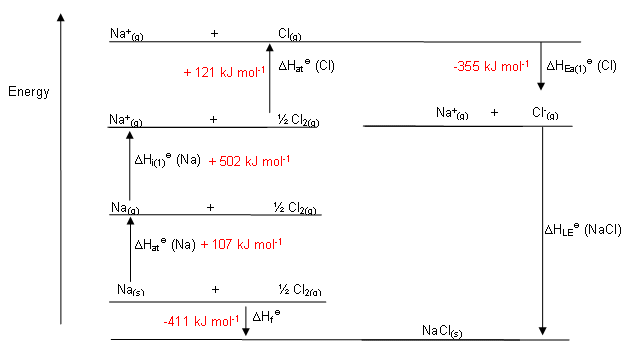
Let's take `"NaCl"` as an example. We begin by writing the formation reaction, which is by definition from the elemental states at `25^@ "C"` and `"1 atm"`:

`"Na"(s) + 1/2"Cl"_2(g) -> "NaCl"(s)`

Our goal is to transform the reactants into their ionic gases, as that is the reaction that describes the process for which "lattice energy" is defined.

1. `"Na"(s) -> "Na"(g)` `lArr` sublimation of sodium solid.
2. `"Na"(g) -> "Na"^(+)(g) + e^(-)` `lArr` Ionization of the gas to remove an electron is by definition the ionization energy.
3. `1/2"Cl"_2(g) -> "Cl"(g)` `lArr` chlorine is now made atomic (defines bond energy).
4. `"Cl"(g) + e^(-) -> "Cl"^(-)(g)` `lArr` chlorine was a gas, and now needs to gain an electron, the definition of electron affinity.
5. `"Na"^(+)(g) + "Cl"^(-)(g) -> "NaCl"(s)` `lArr` the formation of the lattice!

Put this all together, with some data, and we get, for `"1 mol"` of `"NaCl"(s)`:

`"NaCl"(s) -> "Na"(s) + 1/2"Cl"_2(g)`, `-DeltaH_(f,"NaCl"(s)) = +"411 kJ"`

`"Na"(s) -> "Na"(g)`, `DeltaH_("sub","Na") = "107 kJ"`

`"Na"(g) -> "Na"^(+)(g) + e^(-)`, `"IE"_(1,"Na"(g)) = "502 kJ"`

`1/2"Cl"_2(g) -> "Cl"(g)`, `1/2DeltaH_("bond","Cl"_2(g)) = 1/2xx"242 kJ"`

`"Cl"(g) + e^(-) -> "Cl"^(-)(g)`, `"EA"_(1,"Cl"(g)) = -"355 kJ"`

`"Na"^(+)(g) + "Cl"^(-)(g) -> "NaCl"(s)`, `DeltaH_"lattice" = ???`

`"-----------------------------------------------------------------------------"`

`"These cancel out completely upon adding, proving"`

`"we have a complete cycle."`

And now if we wish, the lattice energy can be calculated.

http://www.4college.co.uk/

Take the `DeltaH_f^@` step as being upwards to generate a complete cycle, for which `DeltaH_"cycle" = 0` (since `H_f = H_i` for a complete cycle). Therefore, we have this equation:

`0 = DeltaH_"cycle" = DeltaH_(f,"NaCl"(s))^@ + DeltaH_("sub","Na") + "IE"_(1,"Na"(g)) + 1/2DeltaH_("bond","Cl"_2(g)) - "EA"_(1,"Cl"(g)) - DeltaH_"lattice"`

Solving for `DeltaH_"lattice"` usually gives a positive answer, so we take the negative of the answer by convention to get:

`color(blue)(DeltaH_"lattice" -= -|DeltaH_"lattice"|)`

`= color(blue)(-[DeltaH_(f,"NaCl"(s))^@ + DeltaH_("sub","Na") + "IE"_(1,"Na"(g)) + 1/2DeltaH_("bond","Cl"_2(g)) - "EA"_(1,"Cl"(g))])`

where all the numbers you plug in are positive. For example, we'd get:

`color(blue)(DeltaH_("lattice","NaCl"(s)))`

`= -[411 + 107 + 502 + 1/2(242) - 355] "kJ"`

`= color(blue)(-"786 kJ")`