Question #503ff
2 Answers
Explanation:
So, you're dealing with a buffer solution that contains a weak acid,
Before doing any calculation, try to estimate what the pH of the buffer will be relative to the acid's
Notice that you have
#"NaA"_text((aq]) -> "Na"_text((aq])^(+) + "A"_text((aq])^(-)#
you can say that the solution contains
Since the volume of the solution is the same for both species, you can say that the solution will have equal concentrations of weak acid and of conjugate.
When this is the case, the pH of the buffer will be equal to the acid's
You can prove this by using the Henderson - Hasselbalch equation for a weak acid - conjugate base buffer
#color(blue)("pH" = pK_a + log( (["A"^(-)])/(["HA"])))" "# , where
As you can see here, when you have equal concentrations of conjugate base and weak acid, the log term will be equal to
So right from the start, you can say that the pH of this buffer will be equal to
The actual concentrations of the weak acid and of the conjugate base will be
#["HA"] = ["A"^(-)] = "0.20 moles"/"1 dm"^3 = "0.20 M"#
Therefore,
#"pH" = pK_a + log( color(red)(cancel(color(black)("0.20 M")))/color(red)(cancel(color(black)("0.20 M"))))#
#"pH" = color(green)(4.8)#
Notice that you can use this equation to predict how the pH of the buffer will change when you have
- more weak acid than conjugate base
#log( (["A"^(-)])/(["HA"])) < 0 implies "pH" < pK_a#
The solution will be more acidic.
- more conjugate base than weak acid
#log( (["A"^(-)])/(["HA"])) > 0 implies "ph" > pK_a#
The solution will be more basic.
pH = 4.8
Explanation:
Write out the acid dissociation equation:
You have 0.2 mol acid in
You have 0.2 mol salt in
Now we put this information into an ICE chart:
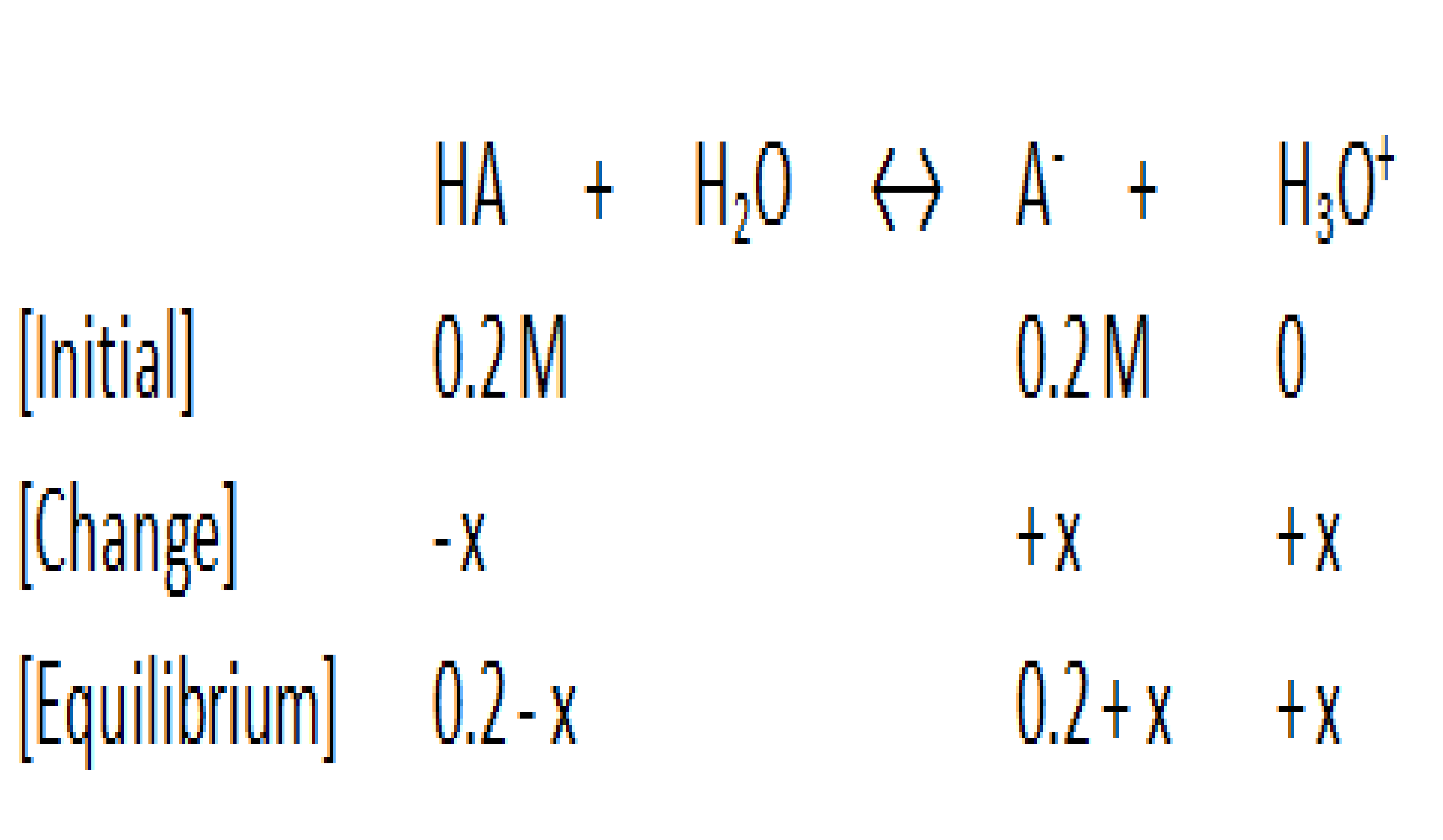
You can eliminate the x in the "0.2-x" and "0.2+x" expressions, because the Ka value in weak acids is very small.
Write out the Ka expression:
Since you need to find the pH, you have to use
Therefore:


