Question #a146a
1 Answer
Here's why that it is so.
Explanation:
The spontaneity of a chemical reaction depends on three factors
These three factors are linked through something called the Gibbs free energy, which is the only criterion that determines whether or not a chemical process if spontaneous or not.
More specifically, you will have
#color(blue)(DeltaG = DeltaH - T * DeltaS)" "# , where
Now, in order for a process to be spontaneous, you need to have
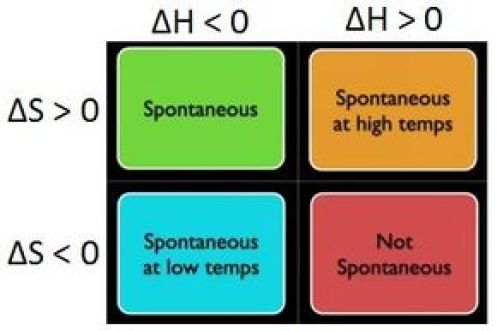
So, looking at the equation for the change in Gibbs free energy, you can say that four distinct scenarios can take place
#DeltaH<0# ,#DeltaS>0 -># spontaneous at any temperature#DeltaH>0# ,#DeltaS<0 -># non-spontaneous regardless of temperature#DeltaH>0# ,#DeltaS>0 -># spontaneous at a certain temperature range#DeltaH<0# ,#DeltaS<0 -># spontaneous at a certain temperature range
So, when solid water, or ice, melts, the process is endothermic, since you need to provide it with heat in order to disrupt the hydrogen bonds that are keeping the water molecules locked in place.
This means that you're in a case where
#DeltaS > 0 -># the entropy of the system is increasing#T# is high enough
So, is the entropy of the system increasing when solid turns to liquid?
Indeed it is!
Remember, entropy is simply a measure of randomness and disorder. When compared with molecules in the solid state, which are vibrating in fixed positions, molecules in the liquid state re free to move around and bump into each other.
So, the only remaining factor that is important here is the temperature at which the reaction takes place,
As it turns out, this value of
You can thus say that
- when
#T < 0^@"C"# , the melting of ice is nonspontaneous, since
#DeltaG = DeltaH - T * DeltaS > 0#
- when
#T > 0^@"C"# , the melting of ice is spontaneous, since
#DeltaG = DeltaH - T * DeltaS < 0#
So, at temperatures above

