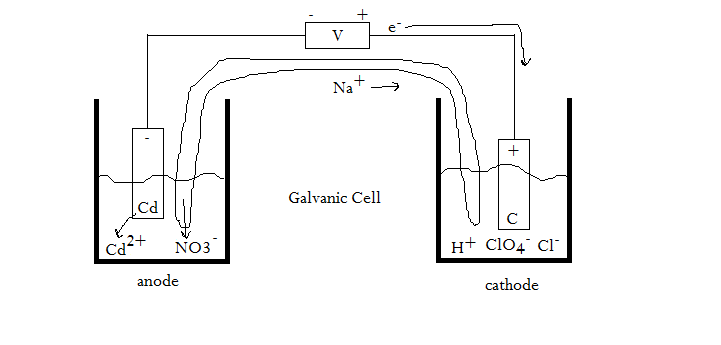
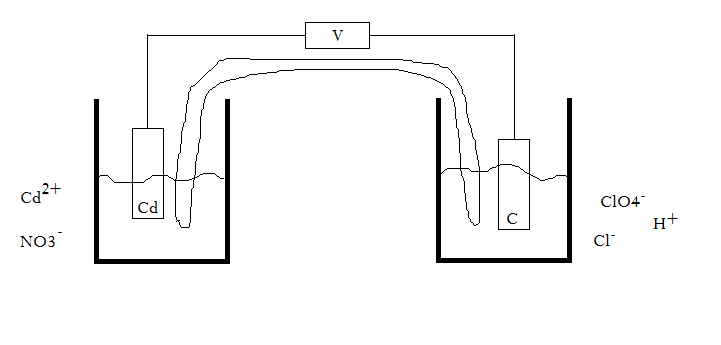
For the cell #"Cd"|"Cd"^(2+), "NO"_3^(-)||"H"^(+), "ClO"_4^(-), "Cl"^(-) | "C"#...?
#a)# Sketch the cell. Write the half-cell reactions and the overall reaction, balanced in acidic media.
#b)# Calculate the cell potential for the overall reaction.
#c)# Calculate the standard change in Gibbs' free energy.
#d)# Is this reaction spontaneous at standard temperature and pressure?
#e)# Sketch the electron and ion flow in the cell in #(a)# .
1 Answer
DISCLAIMER: This is going to be a very long answer.
Well, first let's try drawing this out. Here is a preliminary sketch. We do have to look up the standard reactions though soon.
The carbon electrode, like a platinum electrode, is inert. So that doesn't really do anything in the reaction.
HALF-CELL REACTIONS
Really, it's the
#"Cl"^(-) -> "ClO"_4^(-)#
- Add oxygen to the left side by adding water, because strong acids like these dissociate well in water.
- Add protons to the right side to balance the hydrogens, because we're using acid.
- Add electrons on whichever side helps balance the overall charge.
#color(green)(4"H"_2"O"(l) + "Cl"^(-)(aq) -> "ClO"_4^(-)(aq) + 8"H"^(+)(aq) + 8e^(-))#
#E_"oxid"^@ = -"1.39 V"#
Now the other reaction, which is easier.
#color(green)("Cd"^(2+)(aq) + 2e^(-) -> "Cd"(s))#
#E_"red"^@ = -"0.40 V"# where
#"NO"_3^(-)# is just a spectator ion.
Now, adding them together, we get:
#color(white)(aaa)4["Cd"^(2+)(aq) + cancel(2e^(-)) -> "Cd"(s)]#
#+color(white)(aa)[4"H"_2"O"(l) + "Cl"^(-)(aq) -> "ClO"_4^(-)(aq) + 8"H"^(+)(aq) + cancel(8e^(-))]#
#"-----------------------------------------------------------------"#
#4"Cd"^(2+)(aq) + 4"H"_2"O"(l) + "Cl"^(-)(aq) -> #
#4"Cd"(s) + "ClO"_4^(-)(aq) + 8"H"^(+)(aq)#
I got the half-cell potentials here:
http://www.ed.gov.nl.ca/edu/k12/evaluation/chem3202/standardreductionpotentials.pdf
STANDARD CELL POTENTIAL & STANDARD GIBBS' FREE ENERGY
Alright, so what is the cell potential
Thus, the cell potential we are looking for, apparently, is actually the standard cell potential
We have these relationships involving the standard Gibbs' free energy and the standard cell potential:
#\mathbf(E_"cell"^@ = E_"red"^@ + E_"oxid"^@# (1)
#\mathbf(DeltaG^@ = -nFE_"cell"^@)# (2)where:
#E_"cell"^@# is the standard cell potential at#"1 M"# concentrations and#25^@ "C"# .#E_"red"^@# is the standard reduction potential and#E_"oxid"^@# is the standard oxidation potential (typical charts list reduction potentials);#E_"oxid"^@ = -E_"red"^@# #n# is the number of#"mol"# s of electrons transferred (#8# here)#F# is Faraday's constant (#"96485.3329 C/mol"# )#DeltaG^@# is the standard Gibbs' free energy for the reaction.#"1 V"cdot"C" = "1 J"#
NON-STANDARD GIBBS' FREE ENERGY TELLS YOU THE SPONTANEITY
Remember that
#\mathbf(DeltaG = DeltaG^@ + RTlnQ)# (3)
The train of thought here becomes:
- Figure out
#E_"cell"^@# using (1). - Determine
#DeltaG^@# using (2). - Figure out what
#Q# is. - Determine
#DeltaG# using (3).
IS THE REACTION ABOVE AS-WRITTEN CURRENTLY THE FORWARD OR REVERSE REACTION?
I happen to know that perchloric acid is quite a strong oxidizing agent because it has lots of oxygens.
Thus, we can expect it to oxidize cadmium, and so we should reverse the entire ionic "equation" to get the forward reaction, i.e. the one that would more likely occur.
#color(blue)(4"Cd"(s) + "ClO"_4^(-)(aq) + 8"H"^(+)(aq) -> 4"Cd"^(2+)(aq) + 4"H"_2"O"(l) + "Cl"^(-)(aq))#
Relative to the standard reduction potentials chart I referenced, the perchlorate reaction is now forwards (switch the sign of
Since
Using (1):
#color(green)(E_"cell"^@) = "1.39 V" + "0.40 V" = color(green)(+"1.79 V")#
We should note that cadmium is getting oxidized here, and chlorine is getting reduced (
DETERMINING SPONTANEITY
Now, we can get
#color(blue)(DeltaG^@) = -("8" cancel"mol")("96485.3329"# #cancel"C""/"cancel"mol")("1.79 J/"cancel"C")#
#~~# #color(blue)(-1.3817xx10^6# #color(blue)"J"#
Almost there! Now, what's
#Q = (["ClO"_4^(-)]["H"^(+)]^8)/(["Cd"^(2+)]^4 ["Cl"^(-)])#
(Remember to not include solids and liquids.)
However, we were not given any concentrations, so I suppose we have to assume equilibrium... As a result,
Therefore,
SKETCHING THE ELECTROCHEMICAL CELL?
But we're not done. What about our sketch?
Electrons flow towards the positive terminal, which might or might not be the cathode.
In this case, since cadmium is being oxidized, which involves taking away electrons (thus making the charge more positive), the electrons would flow away from cadmium, towards the cathode.
As a result, the cathode is the positive terminal, making this a galvanic cell (as opposed to an electrolytic cell).
At this point, we can revise our initial sketch to get: