Question

Question #7f583

Answer 1

Here's what I got.

Explanation:

The key to this problem is the balanced chemical equation for this neutralization reaction.

`"HX"`, a weak acid, will react with sodium hydroxide, `"NaOH"`, a strong base, to produce water and the salt of the acid's conjugate base, `"NaX"`.

Since you're in aqueous solution, you can simplify the equation by removing the sodium cations, `"Na"^(+)`, which act as spectator ions in the reaction.

`"HX"_text((aq]) + "NaOH"_text((aq]) -> "X"_text((aq])^(-) + "H"_2"O"_text((aq])`

Notice that you have `1:1` mole ratios between all the chemical species that take part in this reaction.

This tells you that for every one mole of strong base added to the weak acid solution, one mole of weak acid is consumed and one mole of conjugate base is produced.

So, your initial solution contains `n` moles of weak acid. You are told you're adding enough sodium hydroxide to neutralize `1/3` of the moles of acid present, which would be equal to

`1/3 * n ->` one third of the number of moles of weak acid

In order to consume `n/3` moles of acid, you need `n/3` moles of strong base. The number of moles of weak acid that remain in solution B will be equal to

`n_"sol B" = n - n/3 = color(green)((2n)/3)`

Remember that consuming `n/3` moles of weak acid and strong base will also produce `n/3` moles of conjugate base. This means that solution B will contain

`"For HX: " (2n)/3" moles"`

`"For X"^(-): color(white)(a)n/3" moles"`

At this point, you should be able to tell that the concentration of the weak acid is twice as high as the concentration of the conjugate base in solution B. Nevertheless, here's how you can prove that.

Let's assume that the volume of solution B is equal to `V` liters. The concentrations of the two species will be

`color(blue)(c = n/V)`

`["HX"] = (2n)/3"moles" * 1/"V L" = ((2n)/3 * 1/V) " M"`

`["X"^(-)] = n/3"moles" * 1/"V L" = (n/3 * 1/V)" M"`

This means that you have

`(["HX"])/(["X"^(-)]) = ((2n)/3 * color(red)(cancel(color(black)(1/V " M"))))/(n/3 * color(red)(cancel(color(black)(1/V " M")))) = (2 color(red)(cancel(color(black)(n))))/3 * 3/color(red)(cancel(color(black)(n))) = color(green)(2)`

Now, in order to find the acid dissociation constant, `K_a`, write the equilibrium reaction that is established when the weak acid is present in aqueous solution

`"HX"_text((aq]) + "H"_2"O"_text((aq]) rightleftharpoons "H"_3"O"_text((aq])^(+) + "X"_text((aq])^(-)`

By definition, `K_a` will be equal to

`K_a = (["H"_3"O"^(+)] * ["X"^(-)])/(["HX"]) = (["X"^(-)])/(["HX"]) * ["H"_3"O"^(+)]`

Since you know that

`["H"_3"O"^(+)] = 4.2 * 10^(-4)"M"`

and that

`(["HX"])/(["X"^(-)]) = 2 <=> (["X"^(-)])/(["HX"]) = 1/2`

you can say that

`K_a = 1/2 * 4.2 * 10^(-4) = color(green)(2.1 * 10^(-4))`

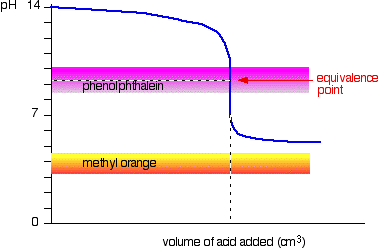
Finally, methyl orange is not a suitable indicator for this titration because at the equivalence point,m the pH of the resulting solution is higher than `7`.

This happens because when all of the weak acid is neutralized, the remaining solution will still contain its conjugate base `"X"^(-)`.

Methyl orange changes color in the `3.1 - 4.4` pH range

which means that it will not be useful for your weak acid - strong base titration. Instead, you should pick an indicator that changes color above `"pH" = 7`, since that's where the equivalence point pH will be for your solution.