Question #3efc2
1 Answer
Gradient is the slope of a graph at point of interest.
For straight line graph it remains same. For curves, it changes as per location of the point of interest.
Explanation:
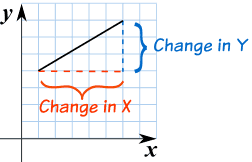
For a straight line graph, select any two points
Calculate,
Recall that for an equation of line in the form
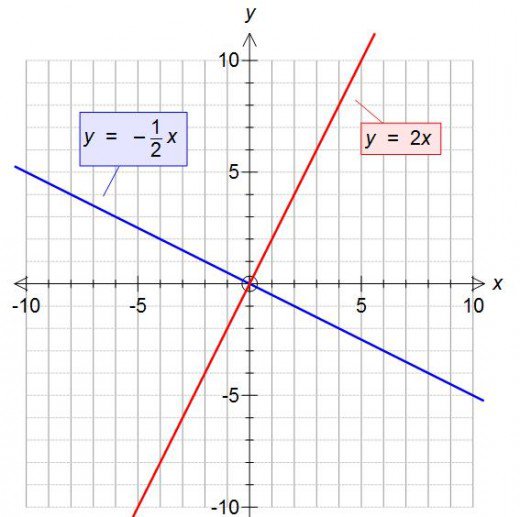
Gradient or slope could be positive or negative as shown in the straight line graphs above. Observe the value of
For curved graphs, one has to draw a tangent at the point of interest. Gradient of the tangent is the gradient of the graph at that point.
This is done by first drawing a line at 90 degrees to the curve at the point where one is required to calculate the gradient of curved graph, a normal or ⊥ line. Then drawing the tangent at 90 degrees to this normal.
