Given
#L->"Length of the rope"=25m#
#M->"Mass of the man climbing"=72kg#
#T->"Tension the rope can withstand"=2.9kN#
Let the sagging be x m when the man is at the mid point of the rope and the rope then subtends angle #theta# with the horizontal.
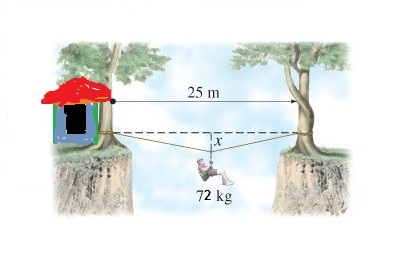
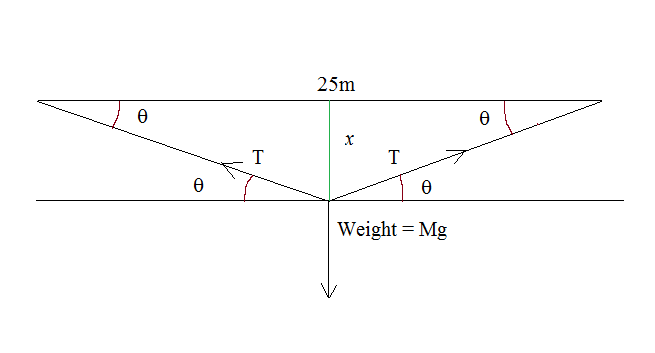
The two vertical components of tension will balance the weight of the man.
So
#2Tsintheta=Mxxg#
#sintheta=(Mg)/(2T).....(1)#
For #theta# being small #sintheta~~tantheta=x/(L/2)=(2x)/L#
Now imposing approximation the relation (1) becomes
#(2x)/L=(Mxxg)/(2T)#
#=>x=(MxxgxxL)/(4T)#
#=>x=(72xx9.8xx25)/(4xx2900)~~1.52m#
Without approximation the realation (1) can be written as
#x/sqrt(x^2+(L/2)^2)=(Mxxg)/(2T)#
#=>(x^2+(12.5)^2)/x^2=((2xx2900)/(72xx9.8))^2=67.57#
#=>1+156.25/x^2=67.57#
#=>156.25/x^2=67.57-1=66.57#
#=>x^2=156.25/66.57#
#=>x=sqrt(156.25/66.57)~~1.53m#
Another way of calculation
From (1)
#theta=sin^-1((Mxxg)/(2T))=sin^-1((72*9.8)/(2*2900))#
#theta=6.99^@#
So
#(2x)/L=tantheta=tan6.99#
#x=(25xxtan6.99)/2=1.53m#



