Question #0465f
1 Answer
Explanation:
You don't have to use a gas law here, all you need to know is Dalton's Law of Partial Pressures.
Dalton's Law of Partial Pressures states that the total pressure of a mixture of gases is equal to the sum of the partial pressures of the components of the mixture.
#color(blue)(P_"total" = sum_i P_i)" "# , where
Now, when you collect a gas over water, you are actually dealing with a gaseous mixture that contains the molecules of said gas and water vapor.
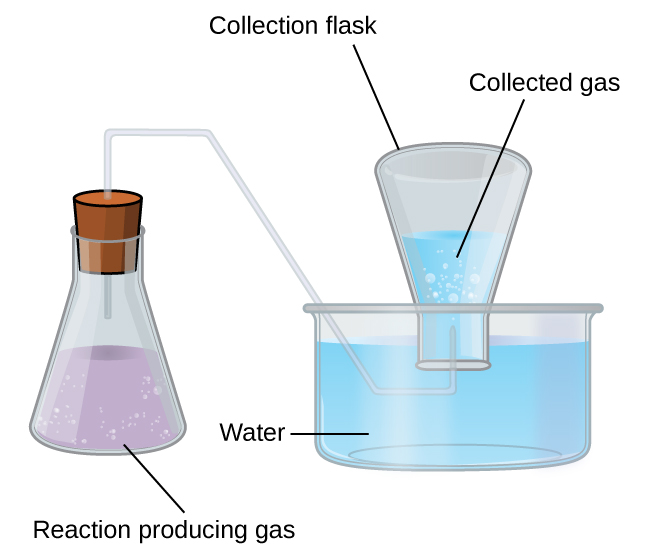
The mixture is referred to as the wet gas. In order to get the partial pressure of the dry gas, you have to account for the fact that the total pressure of the wet gas includes the partial pressure of water at that given temperature.
#P_"wet gas" = P_"dry gas" + P_(H_2O)#
The problem tells you that water has a vapor pressure of
This means that you have
#P_"dry gas" = P_"wet gas" - P_(H_2O)#
#P_"dry gas" = "732 torr" - "42.2 torr" = "689.8 torr"#
You must round this off to the number of decimal places of the least accurate measurement. In your case, that would make the answer
#P_"dry gas"= color(green)("690 torr")#

