This can be rewritten as #intcos^-1x x^-2dx#. Whenever you see a product within an integral, you should consider using integration by parts.
The integration by parts formula states that an integral #intudv = uv - int(v du)#. #cos^-1x# is not that simple to integrate, so let's say #u = cos^-1x# and #dv= x^-2#. Then #du = -1/sqrt(1 - x^2)dx# and #v = -1/x#.
Use the formula now:
#intcos^-1x x^-2dx = -cos^-1x/x - int(-1/x * -1/sqrt(1 - x^2)dx)#
#intcos^-1x x^-2dx = -cos^-1x/x - int 1/(xsqrt(1 - x^2)) dx#
The remaining integral will have to be integrated by trigonometric substitution. This is a technique of integration where you make use of a pythagorean identity to get rid of the #√#. When the square root within the integral is of the form #sqrt(a^2 - x^2)# like the one above, use the substitution #color(red)(x = sin theta)#. Then #dx = costheta d theta#.
#int1/(xsqrt(1 - x^2)) dx= int1/(sinthetasqrt(1 - sin^2theta)) * costheta d theta#
#int1/(xsqrt(1 - x^2))dx =int 1/(sin thetasqrt(cos^2theta)) *costheta d theta#
#int1/(xsqrt(1 - x^2))dx = int1/sintheta d theta#
#int 1/(xsqrt(1 - x^2))dx = intcsctheta d theta#
This is a known integral that is derived here.
#int 1/(xsqrt(1 - x^2))dx = -ln|csctheta + cottheta| + C#
We now reverse the substitutions by drawing a triangle and finding the correct ratios. We know from our original substitution that #x/1 = sintheta#.
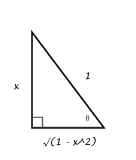
#int 1/(xsqrt(1 - x^2))dx = -ln|1/x + sqrt(1 - x^2)/x| + C#
#int 1/(xsqrt(1 - x^2))dx = -ln|(1 + sqrt(1 - x^2))/x| + C#
Let's return our attention to the whole integral.
#intcos^-1x x^-2dx = -cos^-1x/x- (- ln|(1 + sqrt(1 - x^2))/x|) + C#
#intcos^-1x x^-2dx = ln|(1 + sqrt(1 - x^2))/x| - cos^-1x/x + C#
Hopefully this helps!


