Question #7ec0a
1 Answer
Explanation:
You know that the pressure and the number of moles of gas are kept constant, which means that you can use Charles' Law to find the volume of the gas at standard temperature.
Charles' Law states that the volume and the temperature of a gas have a direct relationship when pressure and number of moles of gas are kept constant.
Simply put, if you increase the temperature of a gas, its volume increases as well. Likewise, if you decrease the temperature of a gas, its volume decreases as well.
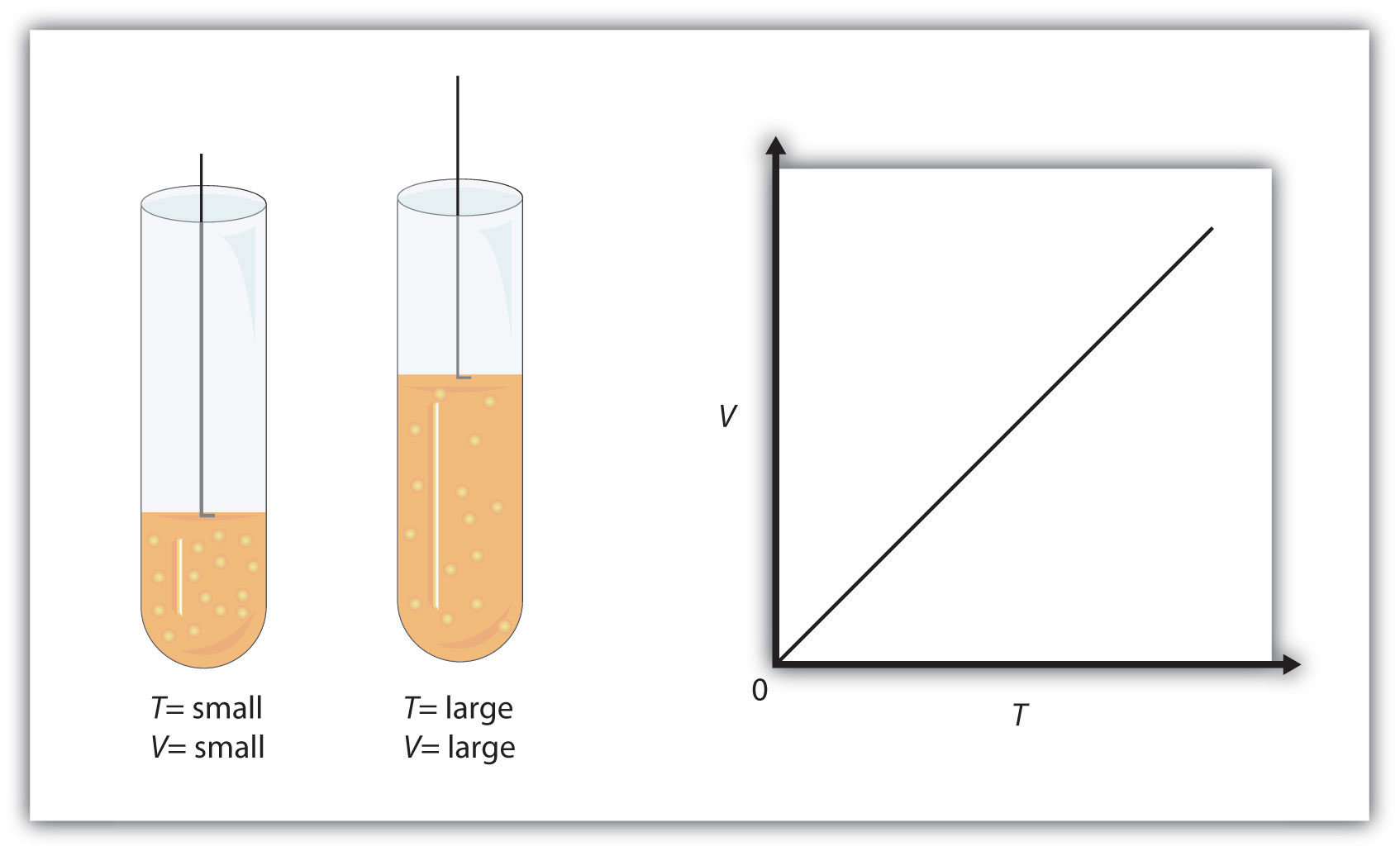
Mathematically, this is written as
#color(blue)(|bar(ul(V_1/T_1 = V_2/T_2))|)" "# , where
Standard Temperature and Pressure conditions are defined as a pressure of
This means that you're decreasing the temperature of the gas from an initial
To convert between degrees Celsius and Kelvin, use the conversion factor
#color(blue)(|bar(ul(color(white)(a/a)T["K"] = t[""^@"C"] + 273.15color(white)(a/a)))|)#
Rearrange the equation that describes Charles' Law to solve for
#V_1/T_1 = V_2/T_2 implies V_2 = T_2/T_1 * V_1#
Plug in your values to get
#V_2 = ((273.15 + 0)color(red)(cancel(color(black)("K"))))/((273.15 + 25)color(red)(cancel(color(black)("K")))) * "725 mL" = "664.21 mL"#
Rounded to two sig figs, the number of sig figs you have for the initial temperature of the gas, the answer will be
#V_2 = color(green)(|bar(ul(color(white)(a/a)"660 mL"color(white)(a/a)))|)#

