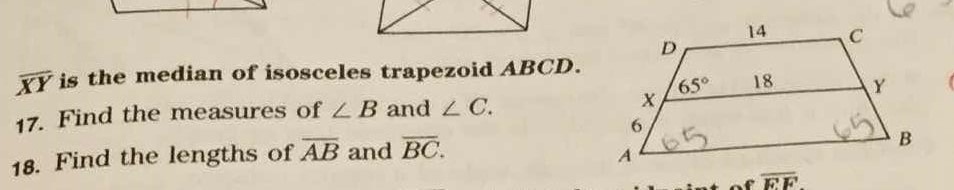
Let's summarize what we know about this object.
#DC||XY||AB#
#/_DXY=65^o#
#DX=XA=6#
#DC=14#
#XY=18#
Draw a line through point #D# parallel to line #BC#. It intersects #XY# at point #Z# and it intersects #AB# at point #E#.
Quadrilateral #CDZY# parallelogram since opposite sides are parallel. Therefore, #YZ=CD=14# and #XZ=XY-YZ=18-14=4#.
Consider #Delta DXZ#. We know its two sides #DX=6# and #XZ=4# and an angle between them #/_DXZ=65^o#. Therefore, we can determine any element of this triangle.
Side #DZ# can be determined using the Law of Cosines:
#DZ^2=DX^2+XZ^2-2*DX*XZ*cos(/_DXZ)#
#DZ^2=6^2+4^2-2*6*4*cos(65^o)=52-48cos(65^o)#
#DZ=sqrt(52-48cos(65^o))#
Angle #/_DZX# can be determined using the Law of Sines:
#(DZ)/sin(/_DXZ)=(DX)/sin(/_DZX)#
or, since we know all elements of this triangle,
#sqrt(52-48cos(65^o))/sin(65^o)=6/sin(/_DZX)#
and, therefore,
#sin(/_DZX)=(6sin(65^o))/sqrt(52-48cos(65^o))#
Since #DZ||BC #, #/_DZX=/_CYX=/_ABC#, so
#sin(/_ABC)=(6sin(65^o))/sqrt(52-48cos(65^o))#
Angle #/_BCD# is, obviously, #180^o-/_ABC#
Triangles #Delta DXZ# and #Delta DAE# are similar since #XZ||AE#. Also note that the factor of scaling between them is #2# since #AD=2*XD#. Therefore, #AE=2*XZ=2*4=8#, which makes
#AB=AE+EB=8+14=22#
Since #DZ=CY=(BC)/2#,
#BC=2*DZ=2*sqrt(52-48cos(65^o))#
I do recommend you to check all my calculations.