Question #6ccf9
1 Answer
Mar 11, 2016
Dividing fractions is done by multiplying the reciprocal of the divisor.
Explanation:
First let's make sure we know which is the divisor:
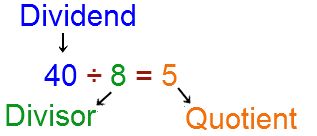
When using fractions, we simply convert the division into a multiplication by taking the reciprocal of the divisor, for example:
If both are fractions, we do the same thing:
which makes sense, since anything divided by itself is one!
PROOF:
to prove this, lets set
now mulitply both sides by
multiply both sides by
therefore

