Question #85772
1 Answer
Here's what I got.
Explanation:
Osmotic pressure is the pressure that must be applied to a solution in order to prevent water from flowing into it through a semi-permeable membrane.
As you know, osmosis is the movement of solvent molecules across a semi-permeable membrane from a region of lower solute concentration to a region of higher solute concentration.
A solution's osmotic pressure will essentially tell you how much pressure must be applied in order to prevent the water molecules from moving across the semi-permeable membrane, i.e. to prevent osmosis.
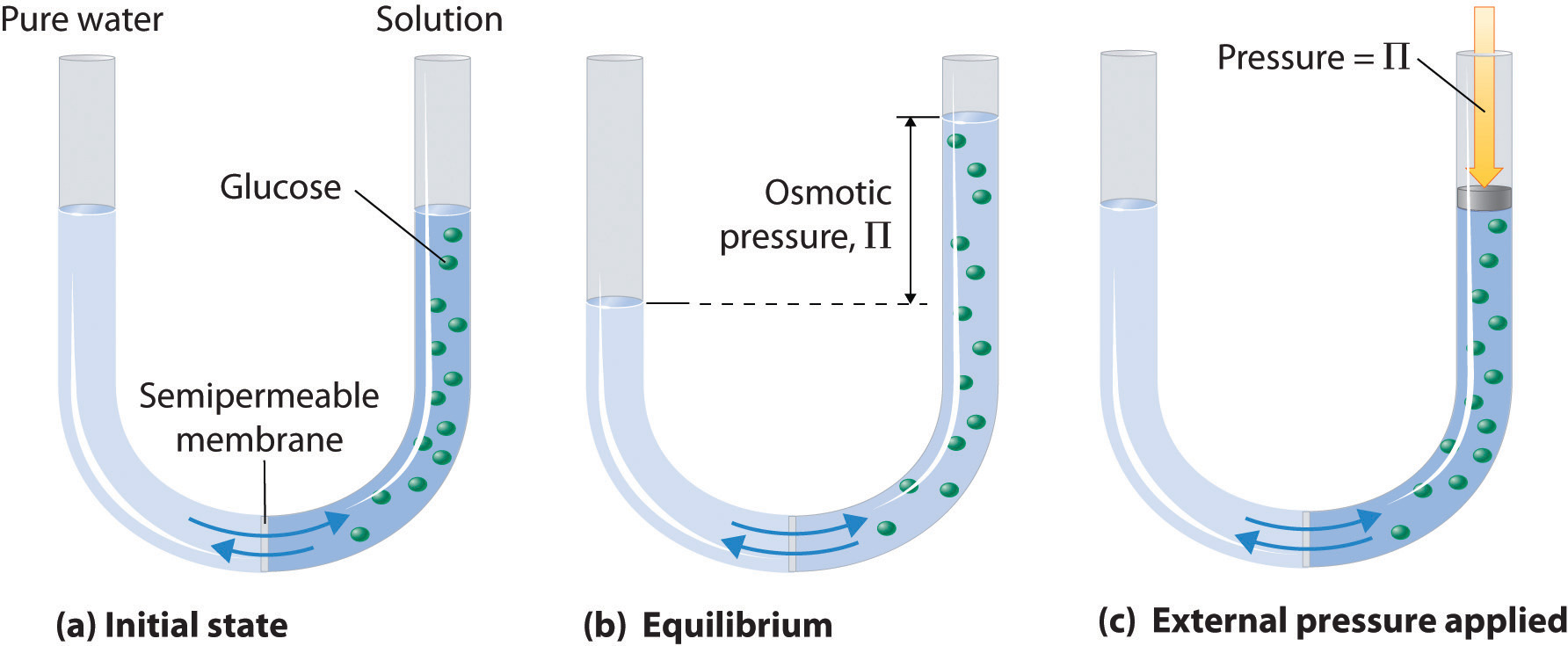
Mathematically, osmotic pressure is defined as
#color(blue)(|bar(ul(color(white)(a/a)Pi = i * c_"solute" * RTcolor(white)(a/a)|)))" "# , where
Now, it's important to remember that osmotic pressure is a colligative property, which means that it depends exclusively on the concentration of solute particles present in solution.
In other words, the nature of the solute is not important, only the concentration of particles it produces in solution.
This is what the van't Hoff factors tells you - how many moles of particles of solute you get per mole of solute added to the solution.
You're dealing with two electrolytes, i.e. soluble ionic compounds
- iron(III) chloride
#-> "FeCl"_3# - potassium chloride
#-> "KCl"#
These two compounds will dissociate in aqueous solution to form cations and anions
#"FeCl"_text(3(aq]) -> "Fe"_text((aq])^(3+) + 3"Cl"_text((aq])^(-)#
#"KCl"_text((aq]) -> "K"_text((aq])^(+) + "Cl"_text((aq])^(-)#
Now, notice that one mole of iron(III) chloride produces one mole of iron(III) cations,
This means that for one mole of solute, you get four moles of solute particles in solution
On the other hand, one mole of potassium chloride produces one mole of potassium cations,
This means that for one mole of solute, you get two moles of particles in solution
The osmotic pressure for these two compounds will be
#Pi_(FeCl_3) = color(red)(4) * "0.1 M" * RT = "0.4 M" * RT#
#Pi_(KCl) = color(red)(2) * "0.2 M" * RT = "0.4 M" * RT#
As you can see, these two solutions have the same osmotic pressure, provided that the temperature is the same.

