Using Raoult's law... and knowing that #A# and #B# form an ideal binary mixture but #R# and #S# have negative deviation...?
#a)# Show that #P_(AB) = P_B^@ + chi_A(P_A^@ - P_B^@)# .
#b)# If #P_A^@ > P_B^@# , #P_A^@ = P_R^@# and #P_B^@ = P_S^@# , sketch a diagram against the mol fraction of #B# for solution #AB# and of #S# for solution #RS# , showing how #P_A# , #P_B# , #P_R# , and #P_S# vary, and how #P_(AB)# and #P_(RS)# look.
1 Answer
Okay, so the idea with this is to compare an ideal binary mixture with a nonideal binary mixture wherein negative deviation occurs upon creation of the mixture.
"SATURATED" VAPOR PRESSURE
If you remember Raoult's law, it dealt with the following relationship:
#\mathbf(P_j = chi_jP_j^@)# where:
#P_j# is the vapor pressure of the solution containing solute (i.e. non-pure).#chi_j = (n_j)/(n_i + n_j)# is the mol fraction of solvent#j# in solution. When#chi_j darr# ,#chi_j < 1# , and#chi_i# , the mol fraction of solute#i# , is increasing.#P_j^@# is the vapor pressure of the solution containing NO solute at all (i.e. purely solvent). This is known as the vapor pressure of the pure solvent, or the "saturated" vapor pressure.
Let's just do the derivation part of the problem right here. Starting from Dalton's law of partial pressures, we just have, for the ideal binary mixture
#P_"tot" = color(blue)(P_(AB)^@) = P_A + P_B#
#= chi_AP_A^@ + chi_BP_B^@#
#= chi_AP_A^@ + (1-chi_A)P_B^@#
#= chi_AP_A^@ + P_B^@ - chi_AP_B^@#
#= color(blue)(P_B^@ + chi_A(P_A^@ - P_B^@))#
The physical interpretation of this result is that the total pressure can be computed for the mixture of any two substances, assuming ideality, by using their pure vapor pressures and by knowing how much
If you look back at how I did this derivation, you should notice that
Thus, you should remember that
ENERGIES OF INTERACTION IN AN IDEAL BINARY MIXTURE
For the ideal binary mixture
#2epsilon_(AB) = epsilon_(A A) + epsilon_(BB)#
This says that the energy of the system after mixing
POSITIVE AND NEGATIVE DEVIATIONS FROM IDEAL MOLAR VOLUMES
Now, we can have two variations on this.
#\mathbf(2epsilon_(AB) < epsilon_(A A) + epsilon_(BB))# (1)
In (1), the energy
That means the particles, after mixing, have a lower overall energy, and thus, mixing is favorable. Thus, the average distance between
That leads to a dip relative to Raoult's law behavior when the mol fraction of the solvent is less than
#\mathbf(2epsilon_(AB) > epsilon_(A A) + epsilon_(BB))# (2)
Similarly, in (2), since the energy for the
That leads to a "hump" relative to Raoult's law behavior when the mol fraction of the solvent is less than
THE AB VS THE RS SOLUTION
Based on your problem setup, what you're dealing with is ideality for the AB solution and negative deviation for the RS solution.
For the ideal mixture, the total vapor pressure,
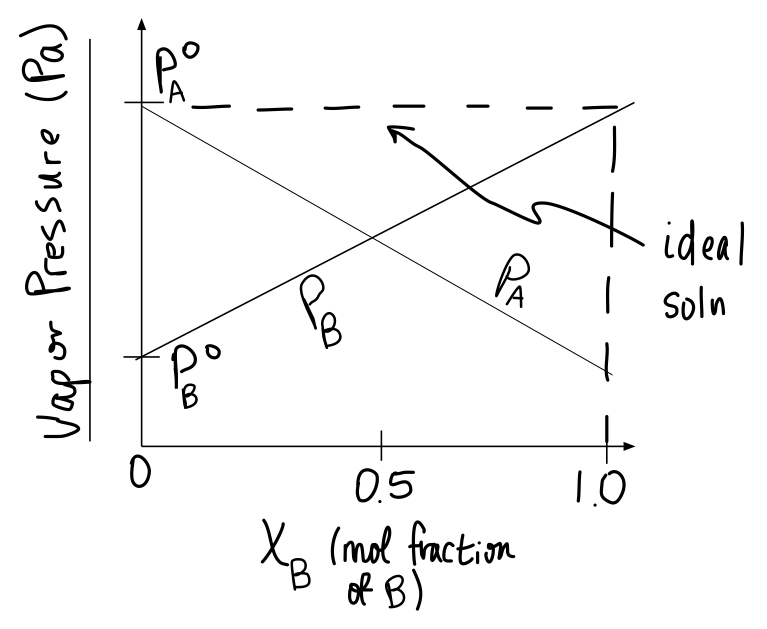
This is because there is no favorability in either the positive or negative direction when it comes to mixing
Note that since we defined
For the
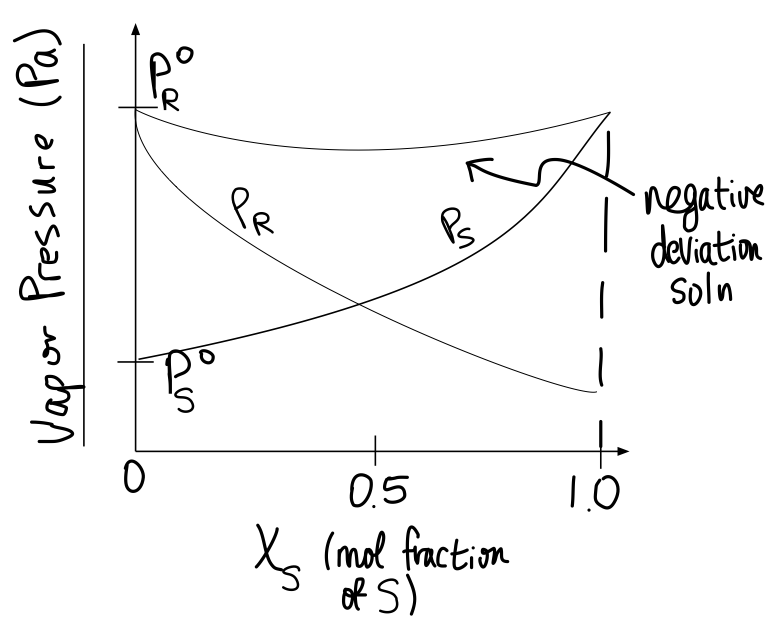
When there is
When there is
Thus,

