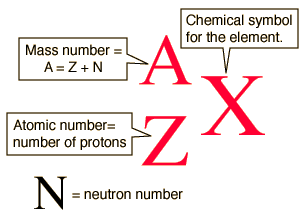Question

Question #b1ea6

Answer 1

Here's what I got.

Explanation:

Isotope notation allows you to identify various isotopes by using atomic number, `Z`, chemical symbol, and mass number, `A`.

So, let's start with antimony-125. Grab a periodic table and look for antimony, `"Sn"`. You'll find it located in period 5, group 14.

Antimony has an atomic number equal to `50`, which means that any atom that contains `50` protons in its nucleus will be an atom of antimony.

Since you know that the given isotope has a mass number equal to `125`, you can say that its isotope notation will be

`color(green)(|bar(ul(color(white)(a/a)color(black)(""_(color(white)(a)50)^125"Sn")color(white)(a/a)|))) ->` antimony-125

Next up, a bismuth nucleus that contains `120` neutrons. Look for bismuth, `"Bi"`, in the periodic table. You'll find it located in period 6, group 16. Bismuth has an atomic number of `83`, which tells you that its nucleus contains `83` protons.

No,w to get he mass number of this isotope, add the number of protons and the number of neutrons located in the nucleus

`A = Z + N`

`A = 83 + 120 = 203`

The isotope notation for this particular isotope will thus be

`color(green)(|bar(ul(color(white)(a/a)color(black)(""_(color(white)(a)83)^203"Bi")color(white)(a/a)|))) ->` bismuth-203

Finally, a nucleus of element 35 that contains `46` neutrons. Once again, pick the a periodic table and look for the element that has an atomic number equal to `35`.

You'll find that this element is bromine, `"Br"`, located in period 4, group 17.

Calculate the isotope's mass number by using the number of protons and the number of neutrons it contains in its nucleus

`A = 35 + 46 = 81`

The isotope notation for this isotope will be

`color(green)(|bar(ul(color(white)(a/a)color(black)(""_ 35^81"Br")color(white)(a/a)|))) ->` bromine-81