Question

Question #72819

Answer 1

`""_ 31^72"Ga" -> ""_ 32^72"Ge" + ""_ "-1"^0"e" + bar(nu)_"e"`

Explanation:

Gallium-72 will undergo radioactive decay via beta minus decay, `beta^(-)`.

Beta minus decay occurs when the nucleus of a radioactive nuclide emits an electron, `"e"^(-)`, also known as a beta particle, and an electron antineutrino, `bar(nu)_"e"`.

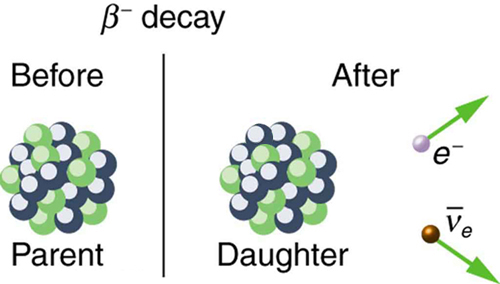
This happens because a neutron located inside the nucleus is converted to a proton.

`color(purple)(|bar(ul(color(white)(a/a)color(black)(""_ 0^1"n" -> ""_ 1^1"p" + ""_ "-1"^0"e" + bar(nu)_"e")color(white)(a/a)|)))`

As a result, the atomic number of the daughter nuclide will increase by `1`, since its nucleus will contain an extra proton.

On the other hand, its mass number, which represents the number of protons and neutrons located inside the nucleus, will remain unchanged.

So, you know that gallium-72 has a mass number equal to `72`. Grab a periodic table and look for the atomic number of gallium, `"Ga"`.

You'll find gallium located in period 3, group 13. Its atomic number is equal to `31`. Look at the element that comes immediately after gallium in the periodic table.

Germanium, `"Ge"`, has an atomic number of `32`. This will be the identity of the daughter nuclide. Since the mass number remains unchanged, the daughter nuclide will be germanium-72.

The beta decay equation will look like this

`color(green)(|bar(ul(color(white)(a/a)color(black)(""_ 31^72"Ga" -> ""_ 32^72"Ge" + ""_ "-1"^0"e" + bar(nu)_"e")color(white)(a/a)|)))`