Question #40610

1 Answer
A08
Jan 21, 2017

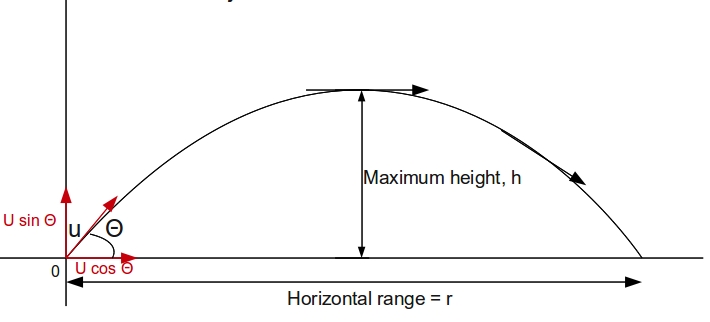
enter image source here
As referred to the figure above.

Kinetic energy at point of projection #KE_"projection"=1/2m u^2#
Maximum height of the object having mass #m# will be reached when #sin theta# component of projectile's velocity becomes #0# (zero).

As such kinetic energy at this point is given by
#KE_"max height"=1/2m(ucos theta)^2#
Ratio of the two is #(KE_"max height")/(KE_"projection")=(1/2m(ucos theta)^2)/(1/2m u^2)#
#=cos^2 theta#

Related questions
See all questions in Projectile Motion
Impact of this question
1720 views around the world
You can reuse this answer
Creative Commons License