Question #c9ca2

1 Answer
Michael
Dec 27, 2016

#sf(rho=1.06color(white)(x)"g/cm"^3)#

Explanation:

From the data on the BCC structure I will work out the mass of 1 sodium atom.

Then I will work out the volume of the FCC unit cell, from which I will work out the density.

BCC refers to "body centred cubic". The unit cell is the smallest unit that, when repeatedly stacked together, will generate the entire structure.

A ball and stick model looks like this:

upload.wikimedia.org

The lines joining the atoms are not bonds in the usual sense. They represent points of contact. Not all the atoms lie inside the unit cell.

There is 1 atom in the centre and at each vertex there is 1/8 of an atom.

This means that the unit cell contains 1 + (8 x 1/8) = 2 atoms.

The side of the unit cell is of length a which we can now calculate.

This will enable us to find the volume of the unit cell which will be #sf(a^3)#.

The direction from a corner of a cube to the farthest corner is called the body diagonal (bd).

The face diagonal (fd) is a line drawn from one vertex to the opposite corner of the same face.

Imagine looking at the unit cell in the plane of the screen from the direction shown:

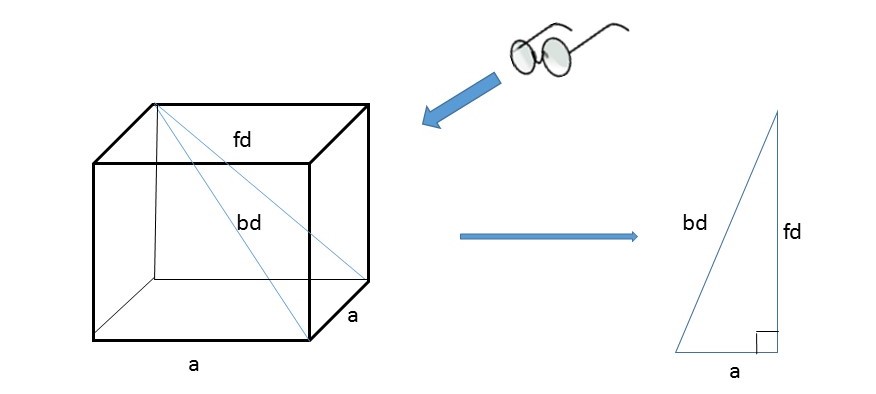
MF Docs

You can see that a right - angled triangle is formed.

Using Pythagoras:

#sf(fd^2=a^2+a^2=2a^2)" "color(red)((1))#

From the diagram we can say also that:

#sf(bd^2=fd^2+a^2)" "color(red)((2))#

From #sf(color(red)((1)))# we can substitute #sf(fd^2)# so #sf(color(red)((2)))# becomes:

#sf(bd^2=a^2+a^2+a^2)#

#:.##sf(bd^2=3a^2)#

The atoms that lie along the body diagonal (bd) touch each other. From the geometry we can say:

#sf(bd=4R)#

Where R is the radius of the atom.

#:.##sf((4R)^2=3a^2)#

#:.##sf(4R=sqrt(3a^2))#

#sf(4R=sqrt(3).a)#

#:.##sf(a=(4R)/(sqrt(3))#

Putting in the numbers:

#sf(a=(4xx180.6xx10^(-12))/(1.732)=417.09xx10^(-12)color(white)(x)m)#

#sf(a=417.09color(white)(x)"pm")#

This is the length of the unit cell.

So the volume V of the unit cell is given by:

#sf(V=a^3=(417.09xx10^(-12))^3=7.2558xx10^(-29)color(white)(x)m^3)#

The mass m of the unit cell is given by:

#sf(m=rhoxxV)#

#:.##sf(m=0.971xx10^3xx7.255xx10^(-29)=7.044xx10^(-26)color(white)(x)kg)#

We have already worked out that there are 2 atoms in the unit cell so the mass #sf(m_(Na))# of 1 atom of sodium is given by:

#sf(m_(Na)=7.044/(2)xx10^(-26)=3.522xx10^(-26)color(white)(x)kg)#

The unit cell for face centred cubic (FCC) looks like this:

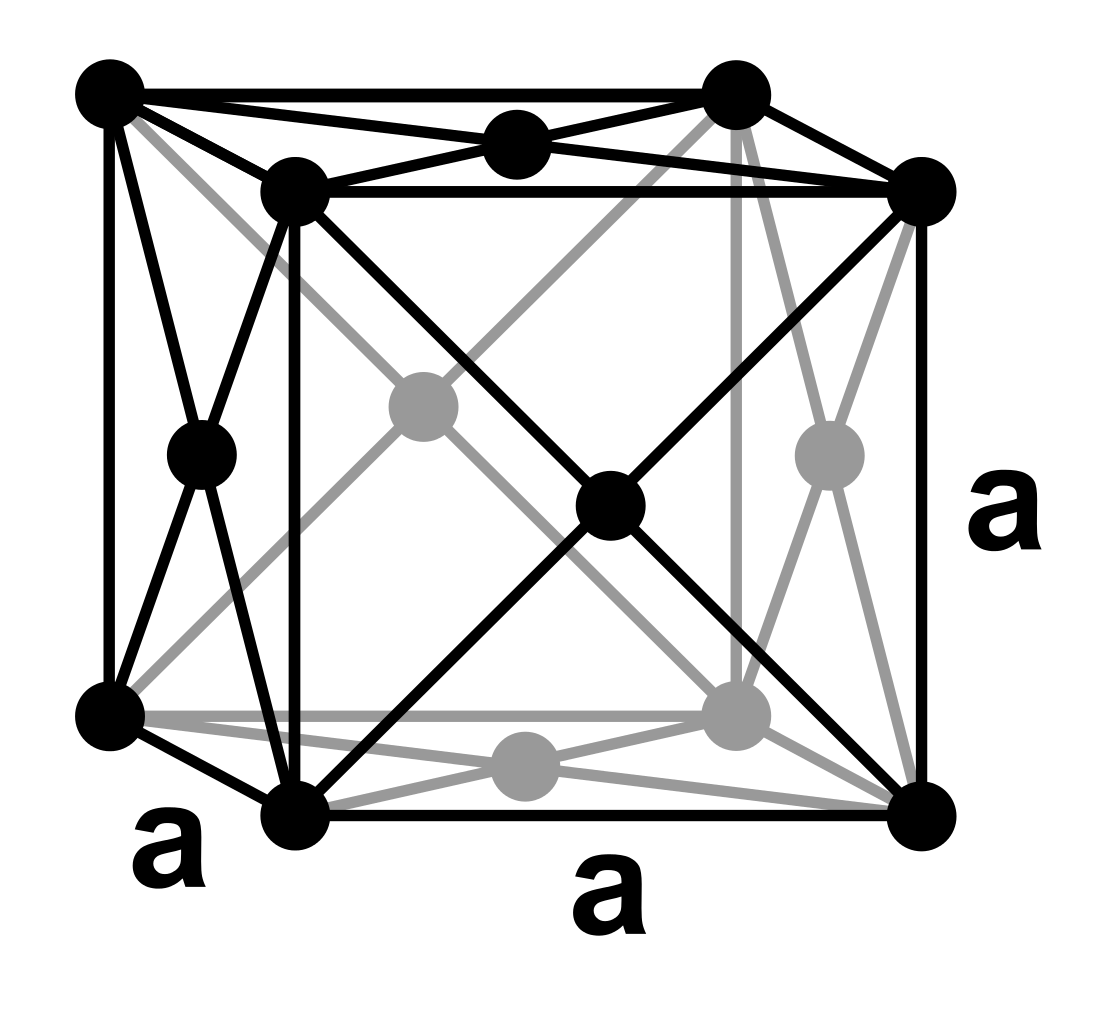
upload.wikimedia.org

You can see that there is an atom at the centre of each face of the unit cell.

Each vertex contains 1/8 of an atom. Each face contains 1/2 of an atom.

So the total no. of atoms in the unit cell will be (8 x 1/8) + (6 x 1/2) = 1 + 3 = 4 atoms.

This can also be seen in the space filling model:

penyayangbercahaya.files.wordpress.com

In the diagram the face diagonal is labelled b.

We can use Pythagoras to find a

Since the atoms are touching we can say that:

#sf(b=r+2r+r=4r)#

Where r is the atomic radius.

From Pythagoras:

#sf(a^2+a^2=(4r)^2)#

#sf(2a^2=16r^2)#

#sf(a^2=8r^2)#

#sf(a=sqrt(8).r)#

#:.##sf(a=sqrt(8)xx180.6xx10^(-12)=510.81xx10^(-12)color(white)(x)m)#

#:.##sf(V_(cell)=(519.81xx10^(-12))^3=1.3329xx10^(-28)color(white)(x)m^3)#

#sf(rho=m_(cell)/V_(cell))#

We have shown that there are 4 atoms in the unit cell so we can write:

#sf(rho=(4xx3.522xx10^(-26))/(1.3329xx10^(-28))=1.0569xx10^(3)color(white)(x)"kg/m"^3)#

#sf(rho=1.06color(white)(x)"g/cm"^3)#

You can see that there is a slight increase in density at this very high pressure as FCC is a more closely packed arrangement.

Related questions
See all questions in Basic Atomic Structure
Impact of this question
2436 views around the world
You can reuse this answer
Creative Commons License