Density

Key Questions

  • How are density mass and volume related?

    Answer:

    They are related by the the density triangle.

    Explanation:

    They are related by the the density triangle.

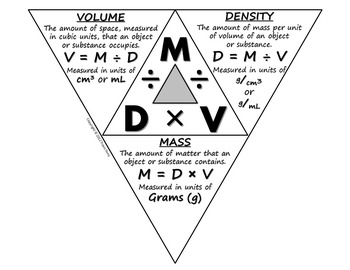
    mcdn1.teacherspayteachers.com

    d = m/VmV

    m = d×V

    V = m/dmd

    DENSITY

    Density is defined as mass per unit volume.

    d = m/VmV

    Example:
    A brick of salt measuring 10.0 cm x 10.0 cm x 2.00 cm has a mass of 433 g. What is its density?

    Step 1: Calculate the volume
    V = lwh = 10.0 cm × 10.0 cm × 2.00 cm = 200 cm³

    Step 2: Calculate the density

    d = m/VmV = (433 g)/(200 cm³) = 2.16 g/cm³

    MASS

    d = m/V

    We can rearrange this to get the expression for the mass.

    m = d×V

    Example:
    If 500 mL of a liquid has a density of 1.11 g/mL, what is its mass?

    m = d×V = 500 mL × (1.11 g)/(1 mL) = 555 g

    VOLUME

    d = m/V

    We can rearrange this to get the expression for the volume.

    V = m/d

    Example:
    What is the volume of a bar of gold that has a mass of 14.83 kg. The density of gold is 19.32 g/cm³.

    Step 1: Convert kilograms to grams.

    14.83 kg × (1000 g)/(1 kg) = 14 830 g

    Step 2: Calculate the volume.

    V = m/d = 14 830 g × (1 cm³)/(19.32 g) = 767.6 cm³

    Ernest Z. · 32 · Jan 11 2014
  • How can density be used to identify substances?

    You can identify an unknown substance by measuring its density and comparing your result to a list of known densities.

    Density = mass/volume. Assume that you have to identify an unknown metal. You can determine the mass of the metal on a scale. You can determine the volume by dropping the object into a graduated cylinder containing a known volume of water and measuring the new volume. You divide the mass by the volume and compare the density to a list of known densities.

    EXAMPLE

    A metal bolt with a mass of 99.7 g is dropped into a graduated cylinder containing 50.0 cm³ of water. The new volume reads
    72.1 cm³. Identify the metal.

    Solution

    V = 72.1 cm³ - 50.0 cm³ = 22.1 cm³

    D = m/V = (99.7 g)/(22.1 cm³) = 4.51 g/cm³

    Now you compare your density with a list obtained from your instructor or from an on-line source such as

    https://sites.google.com/site/chempendix/densities-of-pure-metals

    What metal was your bolt made of?

    Ernest Z. · 259 · Feb 4 2014
  • What is density?

    Answer:

    Density is the mass per unit of volume of a substance.

    Explanation:

    Density measures the compactness in molecular arrangement in any substance which determines how heavy or light any substance is.

    The density formula is "density" = "mass"/"volume". Mass units are most commonly grams or kilograms. Volume units are most commonly cubic centimeters ("cm"^3), cubic meters ("m"^3), or millileters (mL).

    Examples of density include the following:

    The density of water at "4"^"o""C" can be written as "1.000g/cm"^3, "1.000g/mL", "1000Kg/m"^3, and "1.000kg/L".

    The density of iron at "0"^"o""C" is "7.874g/cm"^3 and "7874kg/m"^3.

    The density of sodium metal at "0"^"o""C" is "0.968g/cm"^3, and "968kg/m"^3.

    In order to determine the density of a substance, you need to know its mass and its volume. Then divide its mass by its volume, remembering to divide the units as well.

    Example
    A "1.26cm"^3 sample of the element mercury has a mass of "17.05g". What is it's density?

    Solution

    "density" = "mass"/"volume" = "17.05g"/"1.26cm"^3 =

    "13.5g/cm"^3"

    Here is a video example of how to solve a density problem.

    Meave60 · 9 · Nov 10 2014

Questions

Measurement