the limits from inner integral to outer are
# sqrt(x^2 + y^2) le z le sqrt(2 - x^2 - y^2) qquad star #
# 0 le y le sqrt(1-x^2) qquad square#
#0 le x le 1 qquad triangle#
the limits in #triangle# restrict x to positive values between 0 and 1.
the upper limit in #square # is the equation of a circle in the xy plane of radius 1, ie #x^2 + y^2 = 1#.
And because y is limited as #y ge 0#, this the circle is in the first quadrant of the xy plane as shown in the drawing.
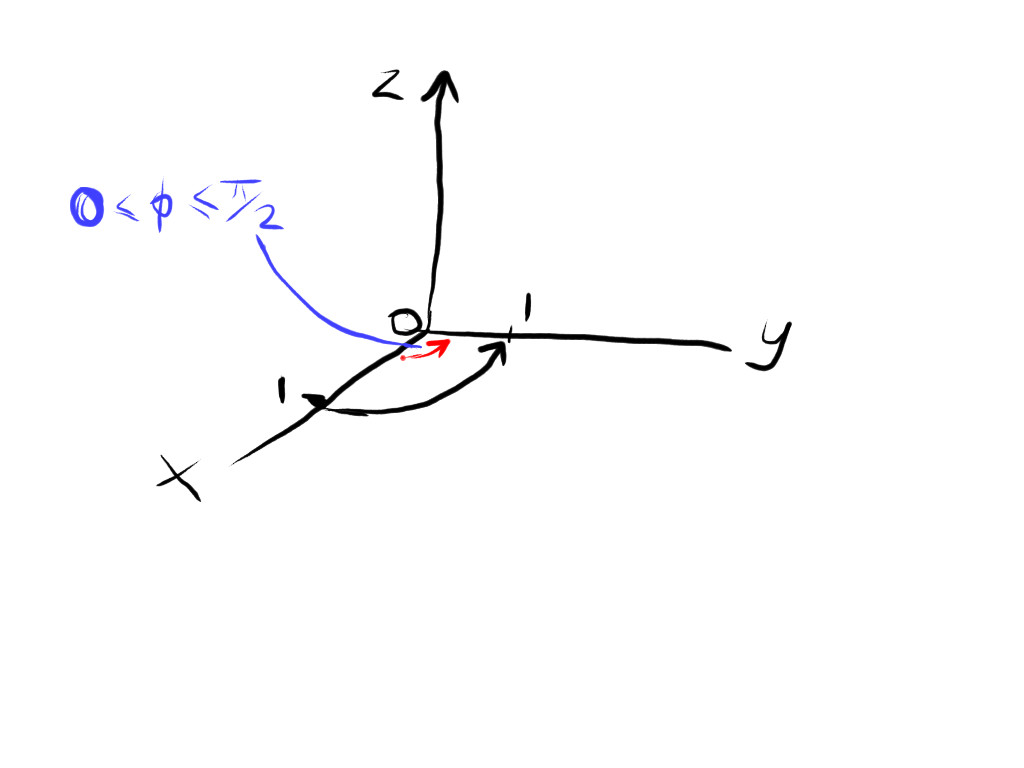
This means that the azimuth angle #phi# is limited as #0 le phi le pi/2#
the first z limit of inner integral in #star# is
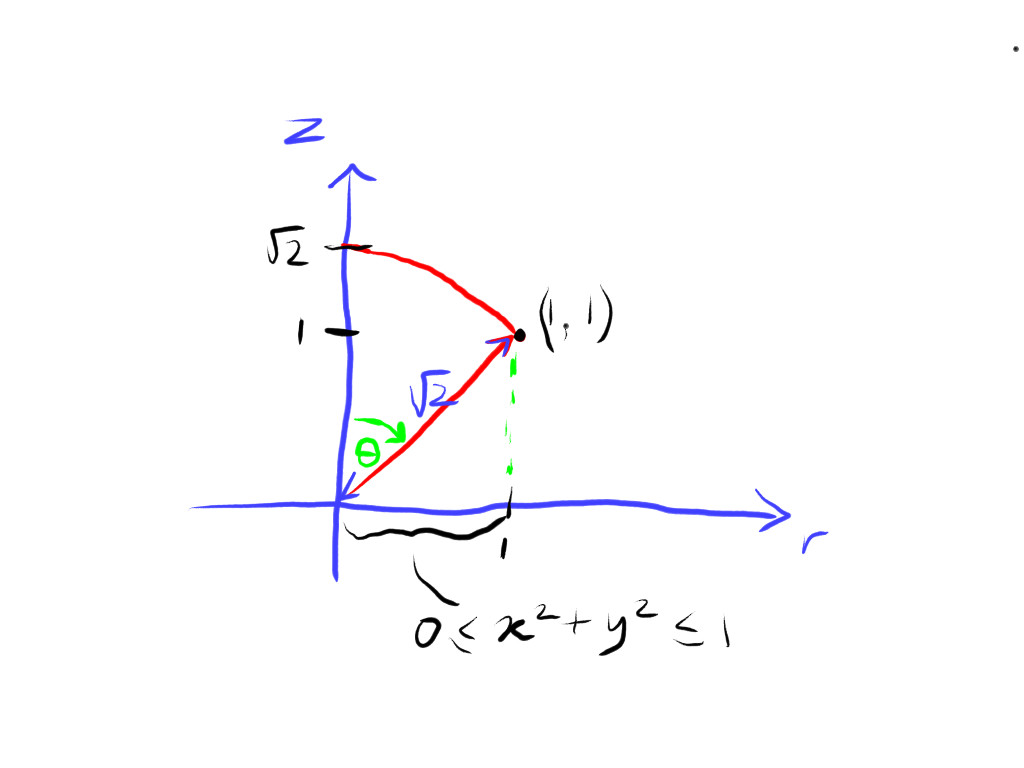
#z = sqrt(x^2 + y^2) #
This is a cone. For example in cylindrical it would be expressed as #z = r#. If you are doing spherical, I assume you must know cylindrical already.
The polar angle is #theta = pi/4# because it is #z=r# with a slope of #(dz)/(dr) = 1#. See the drawing below to note the symmetry.
For the second z limit:
#z = sqrt(2 - x^2 - y^2) implies z^2 +y^2 +z^2 = 2#.
In Cartesian, this is a sphere of radius #sqrt 2#; and in spherical that is expressed simply as #r = sqrt 2#. This is the classic ice cream cone in spherical coordinates
The really crucial bit here is to see that the tip of the cone is within the limits placed on x and y, namely the unit circle. If that was not the case, this would be an entirely different proposition. I hope that the sketch goes some way to showing that.
if we next strip out the limits and begin to replace the integrand and the volume element (including the Jacobian), we have
#int_V xy \ dV#
which becomes
#int_V (r sin theta cos phi)(r sin theta sin phi) \ r^2 sin theta \ dr \ d theta \ d phi#
#= int_V sin^3 theta cos phi \ sin phi \ r^4 \ dr \ d theta \ d phi#
and with limits:
#= int_(theta = 0)^(pi/4) int_(phi = 0)^(pi/2) int_(r = 0)^(sqrt 2) sin^3 theta cos phi \ sin phi \ r^4 \ dr \ d theta \ d phi#



