We need to use the Law of parallelogram of vectors.
The law states that when two vectors (forces) act on a particle at the same time are represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point their resultant vector is represented by the diagonal of the parallelogram in magnitude and direction drawn from the same point.
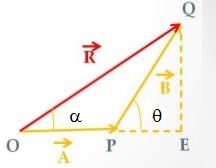
As given in the above figure two forces #vecA and vecB#, inclined at angle #θ#, act on a particle simultaneously. Let these be represented in magnitude and direction by two adjacent sides #OP# and #PQ# of parallelogram drawn from origin #O# (other two sides omitted for simplicity).
According to parallelogram law of vectors, Magnitude and Direction of Resultant #vecR#, obtained by joining tail of #vecA# with tip of #vecB# is found as follows.
Let #vecR # make an angle #alpha# with #x# axis.
Draw perpendicular #QE# on #OP# extended. Considering only the scalar part of the vectors
1. In right #Delta# #QPE#
#PE=B cos theta#
#EQ=B sin theta#
2. In right #Delta# #OQE#
#OE=OP+PE=A+B cos theta#
#R^2=(A+B cos theta)^2+(B sin theta)^2#, using Pythagoras theorem.
#=>R^2=(A^2+B^2 cos^2 theta+2ABcos theta)+(B^2 sin^2 theta)#
#=>R^2=(A^2+B^2 (cos^2 theta+sin^2 theta)+2ABcos theta)#,
simplifying and taking square root of both sides we get
#R=sqrt(A^2+B^2 +2ABcos theta)#
3. #tan alpha=(QE)/(OE)=(B sin theta)/(A+B cos theta)#
#=>alpha=tan^-1 ( (B sin theta)/(A+B cos theta))#
