Can nonpolar molecules have polar bonds?
1 Answer
Sometimes, there can be.
If there is, it must all cancel out. If you consider
#:stackrel(..)"O"="C"=stackrel(..)"O":#
but we should note that it has two dipole moment vectors in the
#stackrel(larr)( :stackrel(..)"O"=)"C"stackrel(rarr)(=stackrel(..)"O": )#
These are of equal magnitude but opposite direction, so they cancel out perfectly. Thus,
However, it doesn't mean
These correspond to
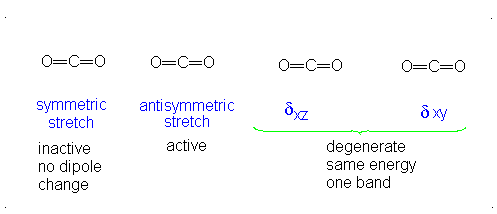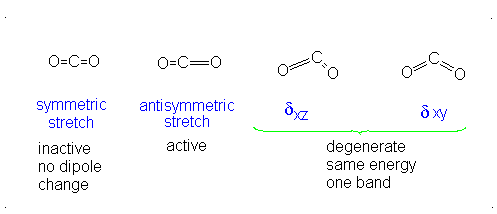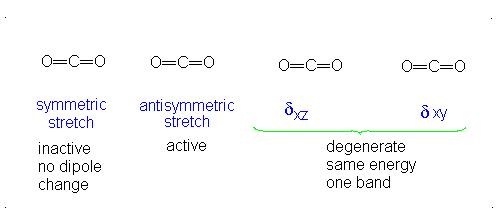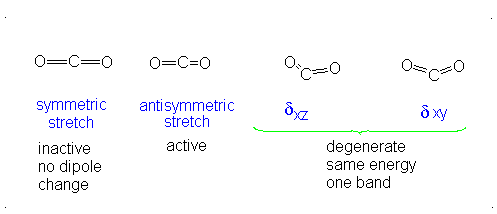
If it were not possible for
We could have treated these identical-magnitude dipole moment vectors as
#vecl + vecr#
#= << 0,0,1 >> + << 0,0,-1 >>#
#= << 0,0,0 >> = vec0#
which is a dot, representing the nonpolar result of two dipole moment vectors of identical magnitude and perfectly opposite directions summing together.

