In a certain test with #k# questions, #a_1# students gave at least one wrong answer, #a_2# students gave at least #2# wrong answers, etc. What was the total number of wrong answers?
2 Answers
Explanation:
This is like the total area of a histogram with the
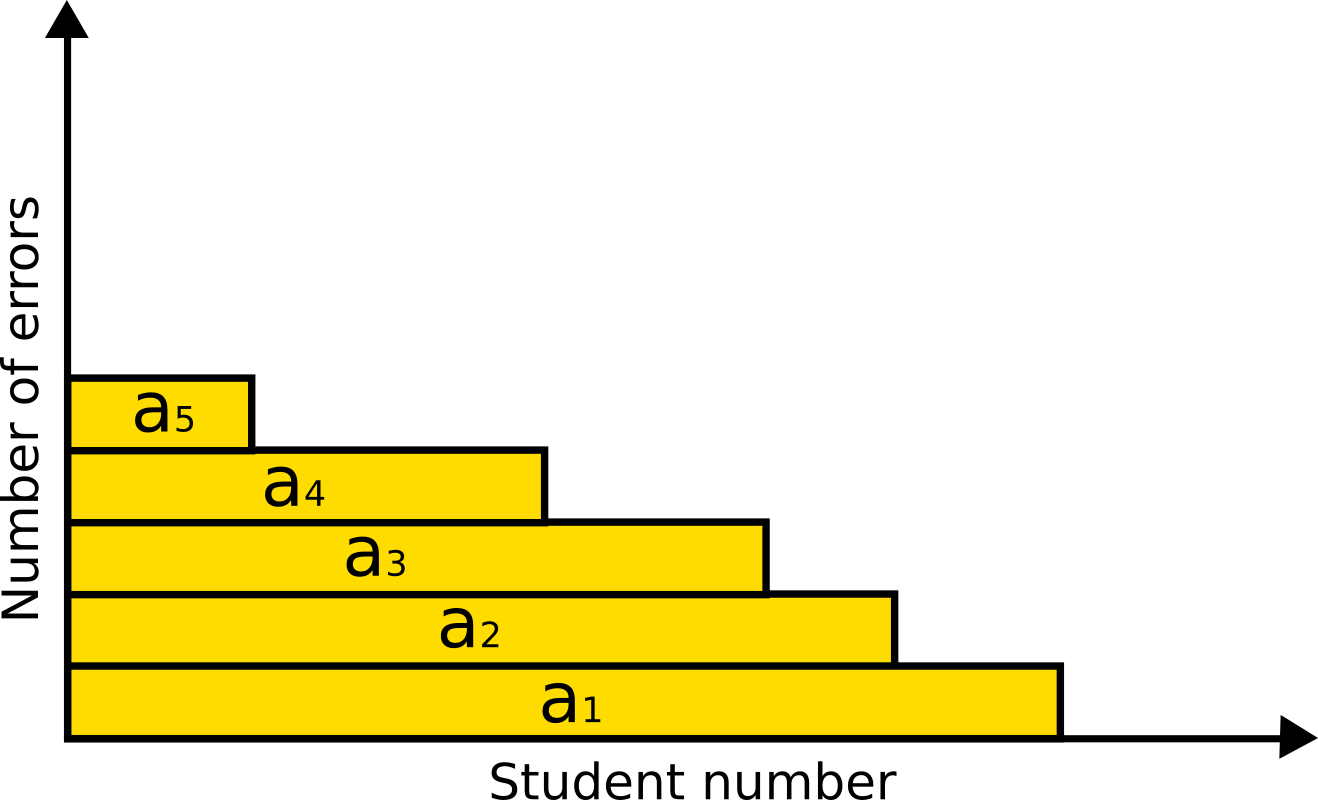
The total number of wrong answer is given by
Explanation:
Note first that if a student gave at least
With the above in mind, we can tell that the number of students who got exactly
With that, we can find the total number of wrong answers by taking the sum over
We could also arrive at the result more quickly by noting that if a student got exactly


