Question

Question #f635a

Answer 1

Here's what I got.

Explanation:

The first part of the question wants you to find a suitable set of quantum numbers for an electron located in a 4f-orbital.

As you know, four quantum numbers are used to describe the position and spin of an electron in an atom.

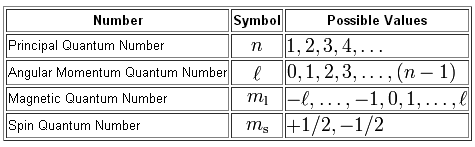
Now, the number that's added to the name of an orbital tells you the energy level on which the electron resides, i.e. the principal quantum number, `n`.

In your case, an electron located in a `color(red)(4)`f-orbital will have `n=color(red)(4)`, which means that it will be located on the fourth energy level.

Now, the angular momentum quantum number, `l`, tells you the subshell in which you can find the electron. You have

• `l=0 ->` the s-subshell
• `l=1 ->` the p-subshell
• `l=2 ->` the d-subshell
• `l=3 ->` the f-subshell

Since your electron is located in the f-subshell, you will need `l = 3`.

At this point, you can have any of the seven values for the magnetic quantum number, `m_l`, that are possible for an electron located in the f-subshell

`m_l = {-3,-2, -1, color(white)(-)0, +1, +2, +3}`

Likewise, the spin quantum number, `m_s`, can take both `-1/2`, which designates an electron that has spin-down, and `+1/2`, which designates an electron that has spin-up.

Therefore, your electron can have

`{(color(white)(a)n = color(red)(4)), (color(white)(a)l= 3), (m_l = {-3, -2, -1, color(white)(-)0, +1, +2, +3}), (m_s = {-1/2, + 1/2}) :}`

For the second part of the question, you must specify the subshell in which the electron is located.

For the first electron, you have `n=2` and `l=1`. This tells you that the electron is located on the second energy level, in the p-subshell, i.e. in one of the three 2p-orbitals.

For the second electron, you have `n=4` and `l=0`. This tells you that the electron is located on the fourth energy level, in the s-subshell, i.e. in the 4s-orbital.