Question

Question #8eea9

Answer 1

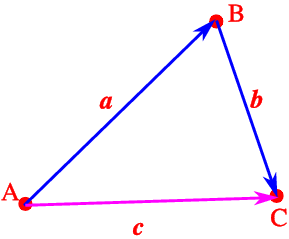
It will be easy to understand the proof of triangle law if we deal this taking displacement as the vector quantity.

Let A be the inltial position of a moving point at an instant. Then after certain time it reaches at B. The length of the straight line AB will represent the magnitude of the displacement and the direction of displacement will be from A to B.So the directed line segment `vec(AB)` is the first displacement vector. Let `vec(AB)=veca`. In the next phase of its movement let it reaches at C after an interval of time. So in 2nd phase of its movement its displacement will be `vec(BC)= vecb("say")`

Hence overall displacement in two phases will be `vec(AC)=vecc("say")`.So the occurrence of two dispacement `veca` and `vecb` in order is equivalent to the displacement `vecc`.

Hence `vecc` is the resultant displacement.

i.e. `veca+vecb=vecc`

And this has been stated in words as triangle law of addition of two vectors in the following way.

when two vectors are represented by two sides of a triangle in magnitude and direction taken in same order then third side of that triangle represents in magnitude and direction the resultant of the vectors.