Question #afdb4
1 Answer
We add the negative of the second vector to the positive of the first to get the magnitude of the resultant vector of
Explanation:
This question asks us to take the difference between two unit vectors where we are only given the angle between them (which we will assume is given in degrees). Let's call our two vectors
Subtracting two vectors graphically is not obvious, so what we can do is replace the vector
so our first equation becomes:
plotting these vectors we get the following (where we have arbitrarily chosen to put vector
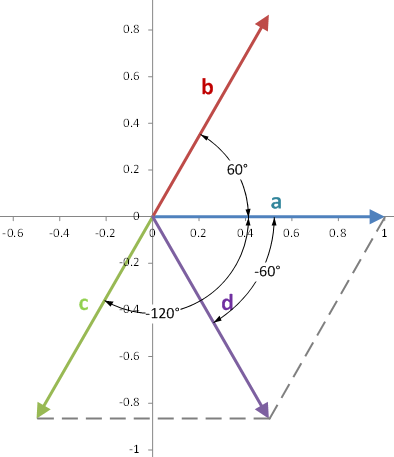
Note that vector
Now we just add
now we add the
The length and angle of
so in polar form, the resultant is
The question asks us for the value of the resulting vector, which we can assume is the magnitude, being

