It is to be noted that the function #psi_n(x)# is normalized wave function. Also #n# can take values as #1,2,3.....# for ground and higher excited states.
Pictorial representation is as below (read #l# for L in the figure).
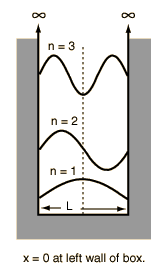
For first excited state #n=2#
Hence, Probability of finding the electron at a point #x# within the width #l# of infinite potential well for #n=2# is
#psi"*"_2 (x)psi_2(x)=2/lsin^2((2pi)/l x)# ......(1)
Probability of finding electron in the first excited state between the values #x=0 and x=0.20xx10^-10m# is definite integral of above equation with respect to variable #x# between the given limits.
#P=int_0^(0.2xx10^-10)psi"*"_2 (x)psi_2(x)dx#
#=>P=int_0^(0.2xx10^-10)2/lsin^2((2pi)/l x)dx#
Using the half angle formula,
#sin^2(x) = 1/2*(1 - cos(2x))# and substituting into the indefinite integral we have
#P=2/lint[1/2(1-cos(2(2pi)/l x))]dx#
#=>P=1/lint(1-cos((4pi)/l x)dx#
#=>P=1/l[intdx-intcos((4pi)/l x)dx]# ......(2)
Now integrating both terms and applying the limits we get
#P=1/l[x-(sin((4pi)/l x))/((4pi)/l)]_0^(0.2xx10^-10)#
#=>P=(0.2xx10^-10)/l-1/(4pi)sin((0.8xx10^-10 pi)/l)#
is the required expression in terms of width #l# of the infinite potential well.
As value of width #l# has not been given, the numerical value of Probability of finding electron in the first excited state between the values #x=0.20xx10^-10m and x=1.00xx10^-10m# can not be calculated.

