How do you solve the quadratic equation #5x^2 + 3x = 1# ?
2 Answers
Explanation:
The first thing to do here is rearrange your equation to quadratic form by getting all the terms on one side of the equation.
To do that, subtract
#5x^2 + 3x - 1 = color(red)(cancel(color(black)(1))) - color(red)(cancel(color(black)(1)))#
#5x^2 + 3x - 1 = 0#
Now, the quadratic formula allows you to calculate the two solutions of a general form quadratic equation
#color(blue)(ax^2 + bx + c = 0)#
by using the equation
#color(blue)(|bar(ul(color(white)(a/a)x_(1,2) = (- b +- sqrt(b^2 - 4 * a * c))/(2 * a) color(white)(a/a)|)))#
In your case, you have
#{(a = color(white)(-)5), (b = color(white)(-)3), (c = -1) :}#
Plug these values into the quadratic formula to get
#x_(1,2) = (-5 +- sqrt(3^2 - 4 * 1 * (-1)))/(2 * 5)#
#x_(1,2) = (-5 +- sqrt(13))/10 implies {(x_1 = (-5 - sqrt(13))/10), (x_2 = (-5 + sqrt(13))/10) :}#
You can thus say that your original equation has two solutions
#x = (-5 - sqrt(13))/10" "# and#" "x = (-5 + sqrt(13))/10#
graph{5x^2 + 3x - 1 [-3, 3, -3, 3]}
Explanation:
Bring the quadratic equation to standard form:
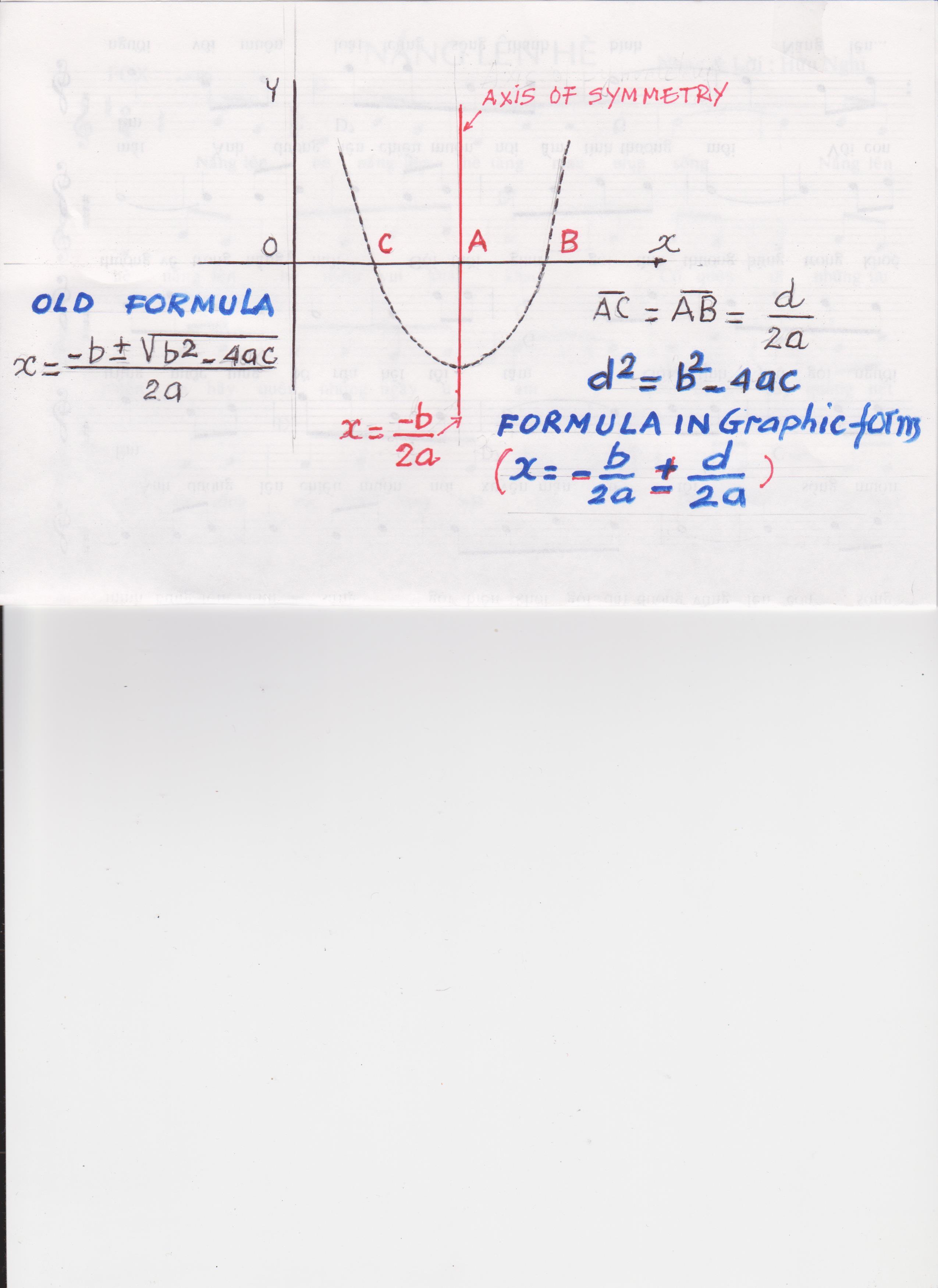
Use the new quadratic formula in graphic form:
There are 2 real roots:
NOTE. Using the improved quadratic formula gets simpler expressions and easier numeric computation. In addition, it shows students the graphic representation and interpretation of the axis of symmetry and the 2 x-intercepts.