Question

Question #079e3

Answer 1

`m_l = 0`

Explanation:

As you know, a total of four quantum numbers can be used to describe the location and spin of an electron inside an atom.

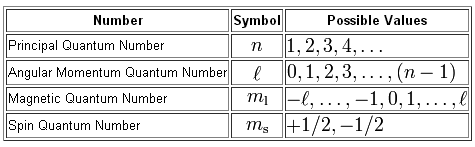
The problem wants you to find the value of the magnetic quantum number, `m_l`, associated with an electron located in the `2s^1` orbital.

Now, the magnetic quantum number tells you the exact orbital in which the electron is located. As you can see, the magnetic quantum number depends on the angular momentum quantum number, `l`< which tells you the subshell in which the electron is located.

Simply put, every subshell will have a different number of orbitals as given be

`m_l = -l, ..., -1, 0, 1, ..., l`

A `2s` orbital is located in the s-subshell, which is given by

`l =0 ->` the s-subshell

As you can see, the magnetic quantum number can only take one possible value for `l=0`, and that is

`m_l = 0 ->` the s-orbital

This tells you that the s-subshell contains a single orbital, the s-oribtal. In this particular case, the `2s` subshell will contain one orbital, the `2s` orbital.