How do you use log tables to find logarithm and the antilogarithm of #445.66# ?
1 Answer
May 25, 2017
Explanation:
Log of
In the log table, find the row for numbers beginning
They will contain numbers like
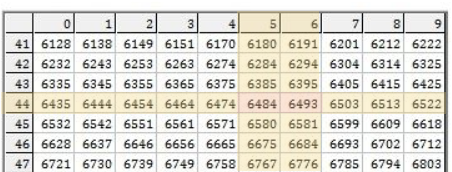
Then since
Hence the logarithm of
Then:
#log(445.66) = log(100*4.4566)#
#= log(100)+log(4.4566) ~~ 2+0.6490 = 2.6490#
Antilog of
In the antilog table against
That tells us that
Hence:
#10^445.66 ~~ 4.571 xx 10^445#

