#{(x^2 + 1 = 81 (y^2 + y)),( x^2 + x = 9 (y^3 + 1)):}#
Solving for #x# both equations
#{(x = pmsqrt[-1 + 81 y + 81 y^2]),(x=1/2 (-1 pm sqrt[37 + 36 y^3])):}#
after squaring and equating
#-21/2 + 81 y + 81 y^2 - 9 y^3 + 1/2 sqrt[37 + 36 y^3]=0#
so we get at
#p(y) = (-21/2 + 81 y + 81 y^2 - 9 y^3)^2 - (1/2 sqrt[37 + 36 y^3])^2# or after expanding
#p(y) =101 - 1701 y + 4860 y^2 + 13302 y^3 + 5103 y^4 - 1458 y^5 + 81 y^6#. and for #x#
#q(x)=19684 + 56862 x + 69987 x^2 - 15309 x^3 - 8745 x^4 + x^6#
Solving iteratively and dividing by the found roots, we get at
#y = {0.0849261,0.146206,9.79971,9.99432}#
and solving correspondingly for #x#
#x = {2.54229,-3.546,-92.5827,94.3364}#
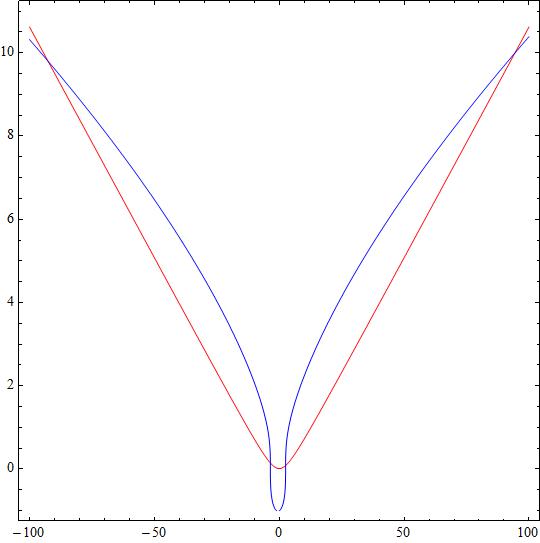
Attached a plot showing the intersections of both curves.
so, the real solution pairs are:
#(
(x= -92.5827, y= 9.79971),
(x= -3.546, y= 0.146206),
(x= 2.54229, y = 0.0849261),
(x= 94.3364, y= 9.99432)
)#