Question #82085
2 Answers
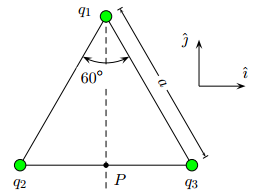
Let charges be
Now according to Coulomb's Law
Inserting given values we get
Similarly
From the figure we see that
Inserting given values we get
From the figure it is clear that angle between the two unit vectors
As such the
Total force is sum of two forces
Explanation:
I will suggest two methods you could use which involves finding the resultant of the two forces acting on the charge.
Here is the situation:
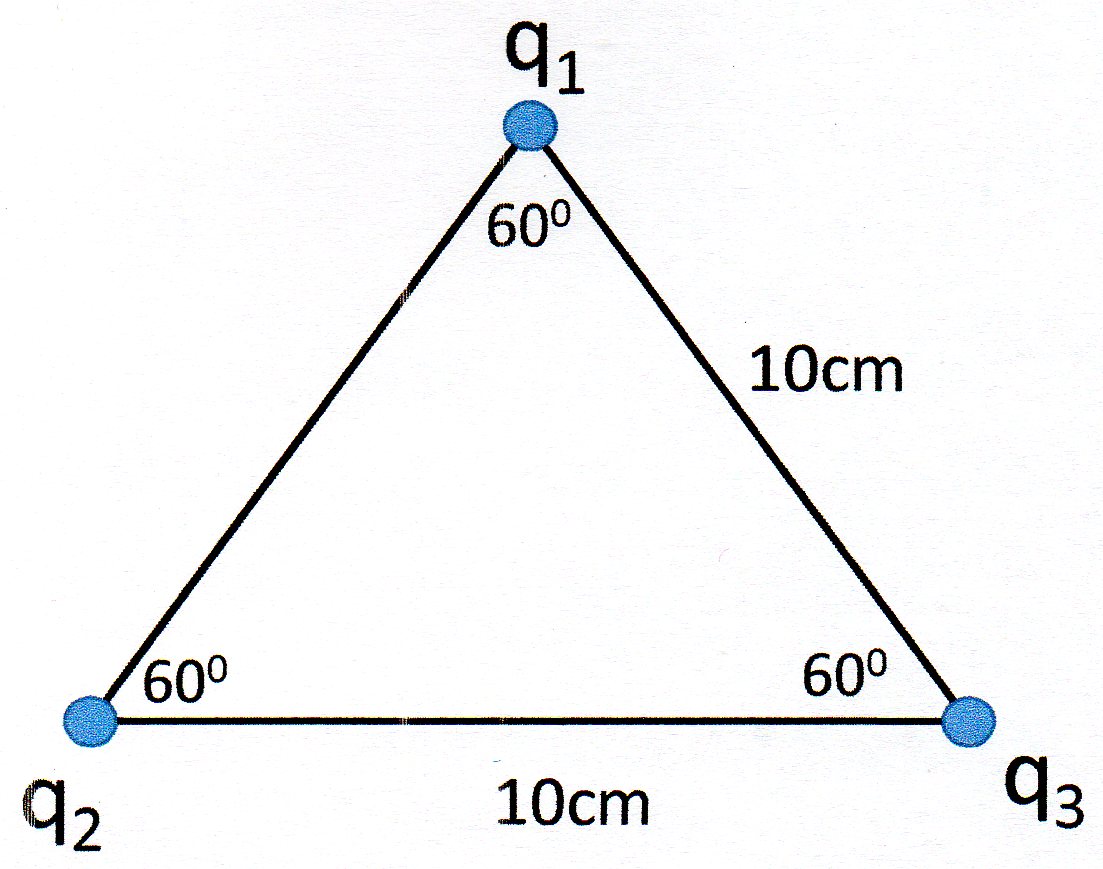
Method (1)
Here is the vector diagram showing the forces acting on
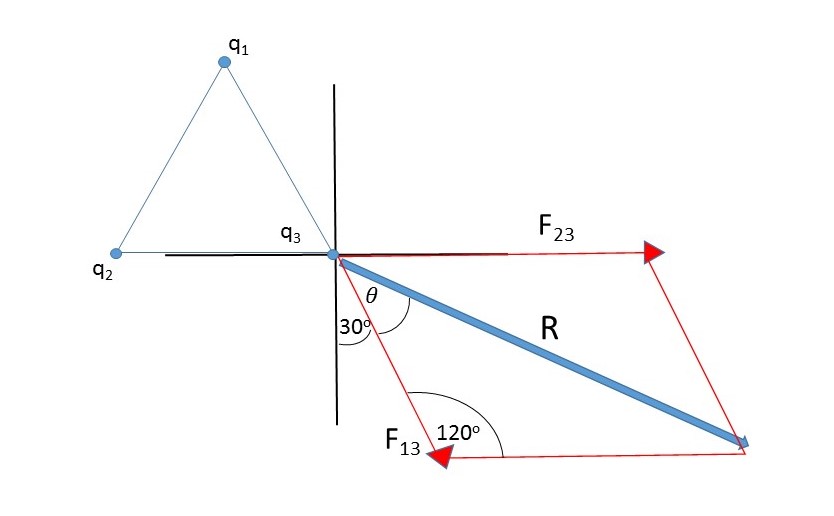
There is a horizontal force
These are indicated by the red arrows. We need to get the resultant R.
Coulombs Law gives us the force of attraction between
By the same reasoning:
To make the numbers easier to handle I will normalise the forces in units of
Now we have a Side Angle Side triangle. We know 2 sides and the angle between them so we can apply the cosine rule to find the unknown side.
For a triangle abc this gives us:
Applying this to the vector diagram we get:
Re-scaling:
To find the angle
From which:
From the diagram you can see that resultant R must be at an angle of
Method (2)
We can resolve the forces into their horizontal and vertical components and find the resultant from that.
Horizontal components:
The horizontal component of
So the total horizontal component is given by:
Vertical components:
Now we can apply Pythagoras:
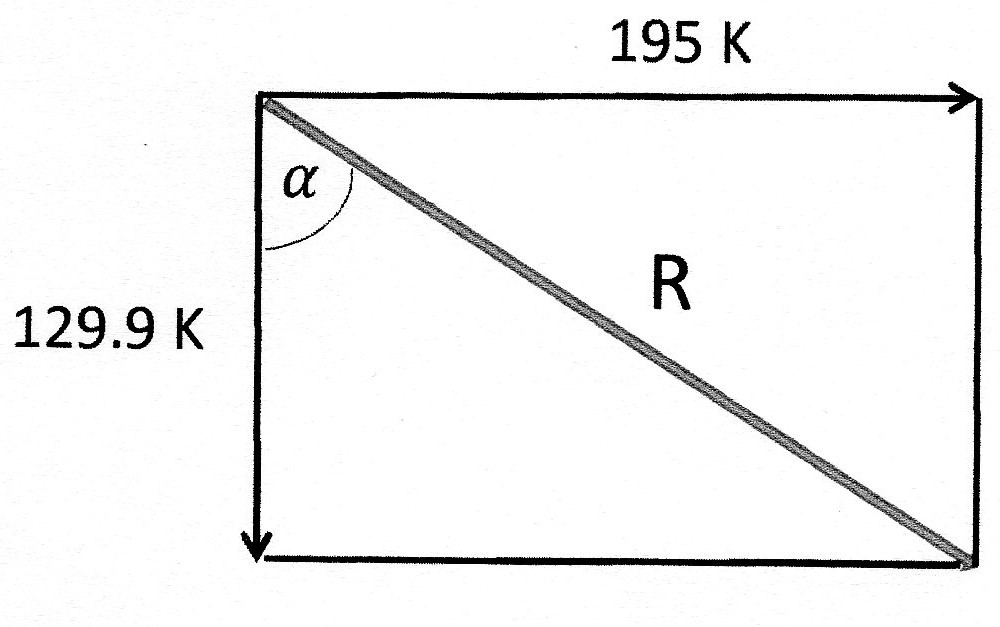
To find the angle
From which:
So the 2 methods are in agreement.

